
Back توزيع برنولي Arabic Bernulli paylanması AZ Размеркаванне Бернулі BE Distribució de Bernoulli Catalan Alternativní rozdělení Czech Κατανομή Μπερνούλλι Greek Bernoulli distribution English Distribución Bernoulli Spanish Bernoulliren banaketa EU توزیع برنولی FA
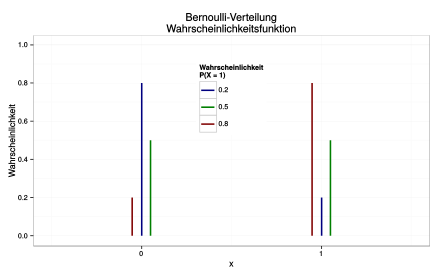
Zufallsvariablen mit einer Bernoulli-Verteilung (auch als Bernoullische Verteilung[1], Null-Eins-Verteilung[1], Alternativ-Verteilung[2] oder Boole-Verteilung[3] bezeichnet) benutzt man zur Beschreibung von zufälligen Ereignissen, bei denen es nur zwei mögliche Versuchsausgänge gibt. Einer der Versuchsausgänge wird meistens mit Erfolg bezeichnet und der komplementäre Versuchsausgang mit Misserfolg. Die zugehörige Wahrscheinlichkeit für einen Erfolg nennt man Erfolgswahrscheinlichkeit und die Wahrscheinlichkeit eines Misserfolgs. Beispiele:
- Werfen einer Münze: Kopf (Erfolg), , und Zahl (Misserfolg), .
- Werfen eines Würfels, wobei nur eine „6“ als Erfolg gewertet wird: , .
- Betrachte sehr kleines Raum/Zeit-Intervall: Ereignis tritt ein , tritt nicht ein .
Die Bezeichnung Bernoulli-Versuch (Bernoullian trials nach Jakob I Bernoulli) wurde erstmals 1937 in dem Buch Introduction to Mathematical Probability von James Victor Uspensky verwendet.[4]
- ↑ a b P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, S. 527.
- ↑ Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1, S. 63, doi:10.1007/978-3-642-45387-8.
- ↑ Klaus D. Schmidt: Maß und Wahrscheinlichkeit. 2., durchgesehene Auflage. Springer-Verlag, Heidelberg Dordrecht London New York 2011, ISBN 978-3-642-21025-9, S. 254, doi:10.1007/978-3-642-21026-6.
- ↑ James Victor Uspensky: Introduction to Mathematical Probability, McGraw-Hill, New York 1937, Seite 45










