Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Bravais-Gitter
Die Bravais-Gitter sind eine Einteilung der möglichen Gittersysteme (Translationsgruppen) in der Kristallographie:
mit ganzen Zahlen und linear unabhängigen Vektoren (im Fall von drei Dimensionen), die das Gitter aufspannen (primitive Vektoren). Bravais-Gitter sind Teil der Klassifikation der Raumgruppen (und die mathematische Ableitung der Klassifikation der Bravais-Gitter findet sich in der zugehörigen Literatur).[1] Die Bravais-Gitter sind also eine Klassifikation der möglichen Translationsgruppen regelmäßiger Punktgitter.[2]
In drei Dimensionen gibt es vierzehn Bravais-Gitter.[3]
Bei der Darstellung der Bravais-Gitter geht man traditionell von den Punktgruppen und deren Einteilung in sieben Kristallsysteme (bzw. 32 Kristallklassen, Typen von Punktgruppen) aus. Aus der Basiszelle des Kristallsystems entstehen die Bravais-Gitter durch Translation und sie werden durch Addition weiterer Gitterpunkte zur Basiszelle konstruiert. Hierbei ist die Basiszelle der Symmetriegruppe des Kristallsystems angepasst (vergleiche die Diskussion bei Elementarzelle und die Darstellung weiter unten). Für die Bravais-Gitter müssen im Allgemeinen noch weitere Gitterpunkte hinzugefügt werden (die als Ausgangspunkt gewählte Basiszelle entspricht nicht der primitiven Elementarzelle des Gitters). Das kann auf sechs mögliche Arten geschehen: flächenzentriert – in jeweils gegenüberliegende Seiten (A, B, C) oder in jeder Fläche (F) – raumzentriert (I) und primitiv (P, das heißt keine Addition von zusätzlichen Gitterpunkten).[4]
Während die Punktgruppen-Symmetrien in der äußeren Kristallform sichtbar sind und aus den Symmetrieelementen Drehung, Spiegelung, Inversion und Drehinversion bestehen, kommen bei der Klassifizierung in den Bravais-Gittern die Translationen hinzu, die im Kristallgitter von mikroskopischer Größenordnung (Ångström) sind und nicht in der äußeren Kristallform sichtbar.
Dabei werden alle Gitterpunkte als gleichwertig betrachtet. Bei der Beschreibung der Kristallstruktur kommt im Allgemeinen zum mathematischen Gitter (definiert über die möglichen Translationen) noch die Beschreibung der Basis hinzu, die auch aus mehreren Atomen bestehen kann (Kristallstruktur ist gleich Gitter plus Basis).
Auguste Bravais klassifizierte um 1849[5] die verschiedenen möglichen Translationsgitter, indem er gleiche parallelepipede Zellen in alle Richtungen aneinander legte. Die Ecken der Zellen ergeben dann ein dreidimensionales Punktgitter, die im realen Kristall die Schwerpunkte der Kristallbausteine (z. B. Atome oder Moleküle) darstellen.
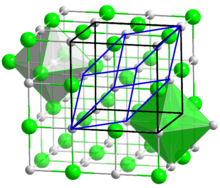
Im Allgemeinen ist das erzeugende Parallelepiped ein schiefes Prisma, bei dem sich alle drei Seitenlängen und Winkel voneinander unterscheiden. In diesem Fall handelt es sich um ein triklines Kristallsystem. Genügen die Seitenlängen und/oder Winkel weiteren Bedingungen, so können sich höhere Symmetrien ergeben. Das kubische Kristallsystem verlangt beispielsweise rechte Winkel und gleich lange Zellkanten. Bravais fiel auf, dass es Gittertypen gibt, die eine Besonderheit aufweisen: Ihre Symmetrie ist höher als an der kleinsten möglichen Zelle ohne weiteres erkennbar wäre. Beim Halit ist es möglich, die halbe Flächendiagonale eines Würfels als Translation zu wählen. Das entstehende Gitter hat jedoch ein Rhomboeder mit dem Winkel von 70° 31' 44" als kleinstes Parallelepiped. Aus Symmetriegründen ist es viel zweckmäßiger, aus dem Gitter einen Würfel als sogenannte Elementarzelle herauszugreifen. Diese kubische Elementarzelle ist größer als der Rhomboeder und enthält in der Mitte jeder Fläche einen weiteren Gitterpunkt. Dieses Gitter wird kubisch flächenzentriert genannt.
- ↑ z. B. Johann Jakob Burckhardt Die Bewegungsgruppen der Kristallographie, 2. Auflage, Birkhäuser, 1966.
- ↑ Okrusch, Matthes Mineralogie, Springer Verlag 2005, S. 9f.
- ↑ Helmut G. F. Winkler (1950): Hundert Jahre Bravais Gitter. In: Die Naturwissenschaften, Band 37, Nummer 17, Seiten 385–390 doi:10.1007/BF00738360.
- ↑ Sanat Chatterjee Crystallography and the World of Symmetry, Springer Verlag 2008, S. 28f (Abschnitt Bravais-Gitter).
- ↑ Bravais: Abhandlung über die Systeme von regelmäßig auf einer Ebene oder im Raum vertheilten Punkten, Leipzig 1897, französisches Original J. Ecole Polytechnique, Band 19, 1850, S. 1–128.
Previous Page Next Page





