Epizykloide

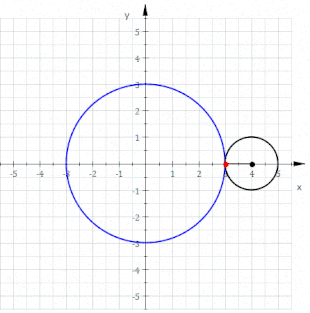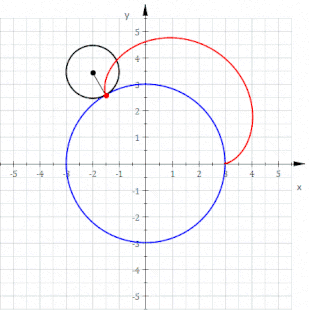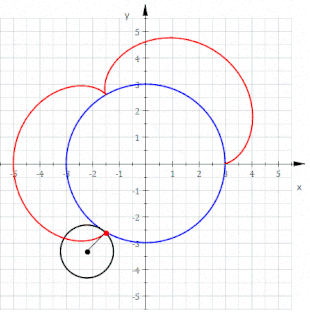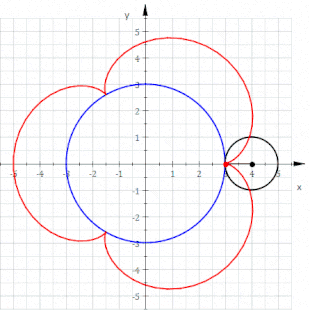
Eine Epizykloide (von altgriechisch ἐπί epí = auf und lateinisch cyclus bzw. altgr. κύκλος kýklos = Kreis) ist eine Rollkurve, die sich folgendermaßen beschreiben lässt: Auf der Außenseite eines gegebenen Kreises (Rastkreis / Rastpolbahn) mit Radius ${\displaystyle R}$ rollt ein weiterer Kreis (Gangkreis / Gangpolbahn) mit Radius ${\displaystyle r}$, ohne zu gleiten. Die Bezeichnungen ${\displaystyle R}$ und ${\displaystyle r}$ sind nicht als Größenvergleich zu verstehen; es gibt auch Epizykloiden mit ${\displaystyle r>R}$. Die Bahn, die ein mitrotierender Punkt auf dem Umfang des Gangkreises beschreibt, wurde schon von Philippe de La Hire als Epizykloide bezeichnet.^[1][2]

Epizykloiden weisen immer Spitzen auf. Befindet sich der mitrotierende Punkt nicht auf dem Umfang des Gangkreises, entstehen Epitrochoiden, also Kurven ohne Spitzen.^[3] Die Epizykloide ist somit ein Spezialfall der Epitrochoiden.

Aufgrund der doppelten Erzeugung kann jede Epizykloide auch durch das Abrollen eines (großen) Kreises um einen fest stehenden kleineren Kreis erzeugt werden. Wenn der Entstehungsmechanismus von Interesse ist, nennt man eine auf diese Art erzeugte Epizykloide eine Perizykloide.^[4] Aus Perizykloiden werden durch kinematische Umkehrung (Vertauschung von festem und bewegtem Kreis) Hypozykloiden. Hier rollt ein kleinerer Kreis auf der Innenseite eines größeren Kreises ab.

Der Begriff Zykloide wird teilweise als Oberbegriff für Hypozykloiden, Epizykloiden, Perizykloiden und Zykloiden verwendet. Bei einer Zykloide handelt es sich aber streng genommen um das Abrollen eines Kreises auf einer Geraden.

Epizykloiden sind blumenähnliche Kurven, die an Mandalas erinnern. Historisch spielten Epizykloiden eine wichtige Rolle in der Epizykeltheorie. Mit dieser Theorie versuchte man, die beobachteten Planeten-Bahnen mit teilweise eigentümlich anmutenden Schleifen zu erklären.

1. ↑ Philippe de La Hire: Traite des Epicycloides et de leur usage dans les mecaniques. 1696, S. 341 (bnf.fr). 
2. ↑ Ludwig Burmester: Lehrbuch der Kinematik, Bd. 1, Die ebene Bewegung. 1888, S. 135 in der Fußnote (digitale-sammlungen.de).  Die finale Namensgebung mit Abgrenzung zu Hypotrochoiden erfolgte allerdings später, 1888 war sie aber dann in der heutigen Form üblich. Ludwig Burmester: Lehrbuch der Kinematik, Bd. 1, Die ebene Bewegung. 1888, S. 139 (digitale-sammlungen.de). 
3. ↑ Die Namensgebung führte Young im Jahr 1800 einYoung: Courxe of lectures, Vol.2. 1800, S. 555.  siehe Fußnote in Ludwig Burmester: Lehrbuch der Kinematik, Bd. 1, Die ebene Bewegung. 1888, S. 138 (digitale-sammlungen.de). 
4. ↑ Weissenborn: Die cyclischen Curven. 1856, S. 3. , siehe Fußnote in Ludwig Burmester: Lehrbuch der Kinematik, Bd. 1, Die ebene Bewegung. 1888, S. 138 (digitale-sammlungen.de).