Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Mitjana
|
|
S'ha proposat que «mitjana (matemàtiques)» sigui fusionat a aquest article. (Vegeu la discussió, pendent de concretar). Data: 2023 |
| Aquest article tracta sobre el concepte estadístic. Vegeu «mitjana (matemàtiques)» pel concepte matemàtic i «mitjana (desambiguació)» per altres significats. |
| No s'ha de confondre amb Mediana (estadística). |
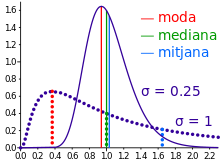
En estadística, el concepte de mitjana té dos significats estretament relacionats:
- El de mitjana aritmètica (que no és el mateix que la mitjana geomètrica o la mitjana harmònica)[1]
- El d'esperança matemàtica d'una variable aleatòria
Hi ha altres mesures estadístiques que no s'han de confondre amb mitjanes, entre elles la mediana i la moda. Altres anàlisis estadístiques simples fan servir mesures de dispersió, com ara l'amplitud, l'amplitud interquartílica o la desviació tipus.
Per una variable aleatòria de valor real X, la mitjana és l'esperança de X. Cal notar que no totes les distribucions de probabilitat tenen una mitjana definida (o variància), com per exemple la distribució de Cauchy.
Per a un conjunt de dades, la mitjana és la suma de tots els valors dividida pel nombre de valors del conjunt. La mitjana d'un conjunt de dades es denota normalment com . Aquesta mitjana és un tipus de mitjana aritmètica. Si el conjunt de dades estigués basat en una sèrie d'observacions obtinguda pel mostreig d'una població estadística, llavors aquesta mitjana s'anomena mitjana mostral () per distingir-la de la mitjana poblacional o x).[2][3] La mitjana se sol donar juntament amb la desviació tipus, ja que la primera descriu la localització central de les dades i la segona en descriu la dispersió. Una mesura alternativa de la dispersió és la desviació mitjana, que equival a la desviació absoluta mitjana de la mitjana: és menys sensible als valors extrems, però matemàticament no és tan amigable per tractar-la.
Si es pren una sèrie d'observacions com a mostra d'una població més gran (per exemple, agafant les alçades d'una mostra d'adults de la població mundial) o bé d'una distribució de probabilitat, llavors la població major es pot utilitzar per construir una "mitjana poblacional" que alhora és el valor esperat per la mostra extreta d'aquesta població. Per una població finita això seria simplement la mitjana aritmètica de la propietat en qüestió per a cada membre de la població; per una distribució de probabilitat, d'altra banda, seria la suma (o integral) sobre cada valor possible ponderat per la probabilitat d'aquest valor. És convenció universal representar la mitjana poblacional per .[4] En cas d'una distribució de probabilitat discreta, la mitjana d'una variable aleatòria discreta x s'obté agafant el producte de cada valor possible de x i la seva probabilitat P(x), i afegint tots aquests valors junts, donant .[5]
La mitjana mostral pot diferir de la mitjana poblacional —especialment per mostres reduïdes—, però la llei dels grans nombres dicta que, com més gran és la mostra, més probable és que la mitjana mostral serà igual a la mitjana poblacional.[6]
Les mitjanes també s'usen en camps diferents de l'estadística, com en geometria i anàlisi, per la qual cosa se n'han desenvolupat molts tipus, els quals es llisten a continuació.
- ↑ Mean. Weisstein, Eric W. MathWorld (anglès)
- ↑ «List of Probability and Statistics Symbols» (en anglès), 26-04-2020. [Consulta: 21 agost 2020].
- ↑ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 0-7021-3838-X p. 181
- ↑ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 070213838X p. 181
- ↑ Elementary Statistics, Robert R. Johnson i Patricia J. Kuby, p. 279
- ↑ Schaum's Outline of Theory and Problems of Probability, Seymour Lipschutz i Marc Lipson, p. 141
Previous Page Next Page






