NP-hard

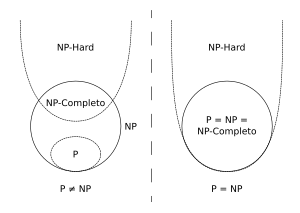
En teoría de la complejidad computacional, la clase de complejidad NP-hard (o NP-complejo, o NP-difícil) es el conjunto de los problemas de decisión que contiene los problemas H tales que todo problema L en NP puede ser transformado polinomialmente en H. Esta clase puede ser descrita como aquella que contiene a los problemas de decisión que son como mínimo tan difíciles como un problema de NP. Esta afirmación se justifica porque si podemos encontrar un algoritmo A que resuelve uno de los problemas H de NP-hard en tiempo polinómico, entonces es posible construir un algoritmo que trabaje en tiempo polinómico para cualquier problema de NP ejecutando primero la reducción de este problema en H y luego ejecutando el algoritmo A.

Asumiendo que el lenguaje L es NP-completo,

1. L está en NP

2. ∀L' en NP, L' ≤ L

En el conjunto NP-Hard se asume que el lenguaje L satisface la propiedad 2, pero no la propiedad 1.

La clase NP-completo puede definirse alternativamente como la intersección entre NP y NP-hard.

Algunas consecuencias de la definición son:

• Como NP-completo es el tipo más costoso de la clase NP, el problema H es al menos tan costoso como NP, pero H no tiene por qué estar en NP y por tanto no tiene por qué ser un problema de decisión.

• Los problemas NP-completos se pueden transformar unos en otros por una reducción polinómica, los problemas NP-completos pueden ser resueltos en tiempo polinómico por reducción a H, así que todos los problemas de NP se reducen a H; sin embargo, esto implica utilizar dos tipos diferentes de transformaciones: de problemas de decisión NP-completos a un problema NP-completo L por transformaciones polinómicas, y de L a H por reducción polinómica de Turing.

• Si hay algún algoritmo polinómico para resolver un problema NP-hard, entonces hay algoritmos para resolver todos los problemas de NP en tiempo polinómico, esto significaría que P=NP.

• Si un problema de optimización H tiene una versión NP-completa, entonces H es NP-hard.

• Si H pertenece a NP, entonces H pertenece también a NP-completo porque en este caso existe una transformación polinómica de Turing que cumple los requisitos de las transformaciones polinómicas.

Un error común es pensar que NP en NP-hard quiere decir no polinómico, ya que aunque hay serias sospechas sobre que no existen algoritmos para resolver estos problemas en tiempo polinómico, esto nunca ha sido demostrado.