Back متطابقة رياضية Arabic Тъждество Bulgarian অভেদ Bengali/Bangla Identitat Catalan Çавахлăх (математика) CV Identitätsgleichung German Αλγεβρικές ταυτότητες Greek Identity (mathematics) English Idento (matematiko) EO Identidad (matemática) Spanish

Unfathiant

Prawf gweledol o gyfathiant Pythagoraidd. Ar gyfer unrhyw ongl θ, mae'r pwynt (cos(θ),sin(θ)) yn gorwedd ar y cylch, sy'n bodloni yr hafaliad x2+y2=1. Felly, cos2(θ)+sin2(θ)=1.

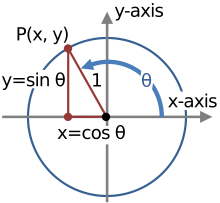
Mewn mathemateg unfathiant (Saesneg: identity) yw perthynas yr hafaledd A = B, fel bod A a B yn cynnwys rhai newidynnau a lle mae A a B yn rhoi'r un gwerthoedd a'i gilydd, ni waeth be fo'r gwerthoedd (rhifau, fel arfer) a gaiff eu cyfnewid am newidynnau. Mewn geiriau eraill, mae A = B yn unfathiant os yw A a B yn diffinio yr un ffwythiannau. Golyga hyn fod yr 'unfathiant' yn 'hafaledd' (equality) rhwng ffwythiannau a ddiffiniwyd yn wahanol. Er enghraifft, mae (a + b)2  =  a2 + 2ab + b2 a cos2(x) + sin2(x) = 1 yn unfathiannau.

Caiff unfathiannau eu dynodi gan y symbol ≡ (bariau triphlyg ), yn hytrach na =, sef yr hafaliad.[1]

  1. ↑ Weiner, Joan (2004).Frege Explained. Open Court.

Unfathiant

Dodaje.pl - Ogłoszenia lokalne