Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group $S̃ 3$

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers ( $..., -2, -1, 0, 1, 2, ...$ ) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 2

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 3

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 4

Bust of Shen at the Beijing Ancient Observatory

Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
Image 5

A stamp of Zhang Heng issued by China Post in 1955

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
Image 6

The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.

In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
Image 7
Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
Image 8
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 9
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 10

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 11
The manipulations of the Rubik's Cube form the Rubik's Cube group.

In mathematics, a group is a set with an operation that associates every pair of elements of the set to an element of the set (as does every binary operation) and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.

Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠ $1$ ⁠ (these properties characterize the integers in a unique way). (Full article...)
Image 12
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 13

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 14

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
Image 15
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.

Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)

Good articles

Image 1
A 1-forest (a maximal pseudoforest), formed by three 1-trees

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.

The names are justified by analogy to the more commonly studied trees and forests. (A tree is a connected graph with no cycles; a forest is a disjoint union of trees.) Gabow and Tarjan attribute the study of pseudoforests to Dantzig's 1963 book on linear programming, in which pseudoforests arise in the solution of certain network flow problems. Pseudoforests also form graph-theoretic models of functions and occur in several algorithmic problems. Pseudoforests are sparse graphs – their number of edges is linearly bounded in terms of their number of vertices (in fact, they have at most as many edges as they have vertices) – and their matroid structure allows several other families of sparse graphs to be decomposed as unions of forests and pseudoforests. The name "pseudoforest" comes from Picard & Queyranne (1982). (Full article...)
Image 2
A Doyle spiral of type (8,16) printed in 1911 in Popular Science as an illustration of phyllotaxis. One of its spiral arms is shaded.

In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.

Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or early 1990s. However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early 1900s. (Full article...)
Image 3
Basic Math is an educational video game for the Atari Video Computer System (Atari VCS). The game was developed at Atari, Inc. by Gary Palmer. The game involves a series of ten arithmetic problems involving addition, subtraction, multiplication, or division. The player can edit different gameplay modes to alter how the numbers in the problem are chosen, or if their questions are timed. The game was released in 1977 as one of the earliest releases for the console.

The game is the only known game developed for the VCS by Palmer, who initially worked at Atari creating debugging stations for game developers, and later assisted with work on the Atari 400/800 line of computers. It was the first educational video game for the VCS, with others companies also releasing arithmetic-themed cartridges in the same year for the Fairchild Channel F and RCA Studio II. The game was also released under the title Fun with Numbers and Math. Both contemporary and retrospective reviews were generally unenthused by the game with common criticism being that it had poor quality graphics and was not appealing in terms of gameplay or control. (Full article...)
Image 4
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.

There are multiple different notations for differentiation, two of the most commonly used being Leibniz notation and prime notation. Leibniz notation, named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas prime notation is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leibniz notation by adding superscripts to the differentials, and in prime notation by adding additional prime marks. The higher order derivatives can be applied in physics; for example, while the first derivative of the position of a moving object with respect to time is the object's velocity, how the position changes as time advances, the second derivative is the object's acceleration, how the velocity changes as time advances. (Full article...)
Image 5
The integer number line, a set of infinitely many points with integer distances. According to the Erdős–Anning theorem, any such set lies on a line.

The Erdős–Anning theorem states that, whenever an infinite number of points in the plane all have integer distances, the points lie on a straight line. The same result holds in higher dimensional Euclidean spaces.
The theorem cannot be strengthened to give a finite bound on the number of points: there exist arbitrarily large finite sets of points that are not on a line and have integer distances.

The theorem is named after Paul Erdős and Norman H. Anning, who published a proof of it in 1945. Erdős later supplied a simpler proof, which can also be used to check whether a point set forms an Erdős–Diophantine graph, an inextensible system of integer points with integer distances. The Erdős–Anning theorem inspired the Erdős–Ulam problem on the existence of dense point sets with rational distances. (Full article...)
Image 6

8x8 Rook's graph

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

Rook's graphs are highly symmetric, having symmetries taking every vertex to every other vertex. In rook's graphs defined from square chessboards, more strongly, every two edges are symmetric, and every pair of vertices is symmetric to every other pair at the same distance in moves (making the graph distance-transitive). For rectangular chessboards whose width and height are relatively prime, the rook's graphs are circulant graphs. With one exception, the rook's graphs can be distinguished from all other graphs using only two properties: the numbers of triangles each edge belongs to, and the existence of a unique $4$ -cycle connecting each nonadjacent pair of vertices. (Full article...)
Image 7
In mathematics and computer science, the BIT predicate, sometimes written ${\text{BIT}}(i,j)$ , is a predicate that tests whether the $j$ th bit of the number $i$ (starting from the least significant digit) is 1, when $i$ is written as a binary number. Its mathematical applications include modeling the membership relation of hereditarily finite sets, and defining the adjacency relation of the Rado graph. In computer science, it is used for efficient representations of set data structures using bit vectors, in defining the private information retrieval problem from communication complexity, and in descriptive complexity theory to formulate logical descriptions of complexity classes. (Full article...)
Image 8
Walton in Pomona College's Walker Lounge c. 1957

Jean Brosius Walton (March 6, 1914 – July 5, 2006) was an American academic administrator and women's studies scholar. She spent the bulk of her career at Pomona College in Claremont, California.

Born to a Pennsylvania Quaker family, Walton grew up at George School and studied mathematics at Swarthmore College, Brown University and the University of Pennsylvania. She joined Pomona College in 1949 as the Dean of Women, and was promoted to dean of students in 1969 and vice president for student affairs in 1976, three years before her formal retirement. During her tenure, she advocated for women's education, engaged with student protests against the Vietnam War, oversaw reform of residential life policies to eliminate parietal rules, and co-founded the Claremont Colleges' Intercollegiate Women's Studies Program. She earned widespread recognition for her work and was praised by colleagues for her independent and dignified personality. (Full article...)
Image 9
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

This result provides a classification theorem for the three-dimensional convex polyhedra, something that is not known in higher dimensions. It provides a complete and purely combinatorial description of the graphs of these polyhedra, allowing other results on them, such as Eberhard's theorem on the realization of polyhedra with given types of faces, to be proven more easily, without reference to the geometry of these shapes. Additionally, it has been applied in graph drawing, as a way to construct three-dimensional visualizations of abstract graphs. Branko Grünbaum has called this theorem "the most important and deepest known result on 3-polytopes." (Full article...)
Image 10
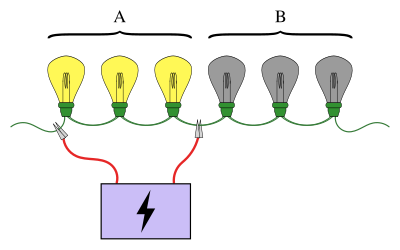
An illustration of the lightbulb problem, where one is searching for a broken bulb among six lightbulbs. Here, the first three are connected to a power supply, and they light up (A). This indicates that the broken bulb must be one of the last three (B). If instead the bulbs did not light up, one could be sure that the broken bulb was among the first three. Continuing this procedure can locate the broken bulb in no more than three tests, compared to a maximum of six tests if the bulbs are checked individually.

In statistics and combinatorial mathematics, group testing is any procedure that breaks up the task of identifying certain objects into tests on groups of items, rather than on individual ones. First studied by Robert Dorfman in 1943, group testing is a relatively new field of applied mathematics that can be applied to a wide range of practical applications and is an active area of research today.

A familiar example of group testing involves a string of light bulbs connected in series, where exactly one of the bulbs is known to be broken. The objective is to find the broken bulb using the smallest number of tests (where a test is when some of the bulbs are connected to a power supply). A simple approach is to test each bulb individually. However, when there are a large number of bulbs it would be much more efficient to pool the bulbs into groups. For example, by connecting the first half of the bulbs at once, it can be determined which half the broken bulb is in, ruling out half of the bulbs in just one test. (Full article...)
Image 11
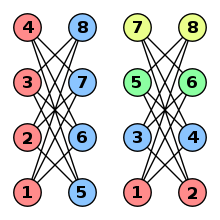
Two greedy colorings of the same crown graph using different vertex orders. The right example generalises to 2-colorable graphs with $n$ vertices, where the greedy algorithm expends $n /2$ colors.

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.

Different choices of the sequence of vertices will typically produce different colorings of the given graph, so much of the study of greedy colorings has concerned how to find a good ordering. There always exists an ordering that produces an optimal coloring, but although such orderings can be found for many special classes of graphs, they are hard to find in general. Commonly used strategies for vertex ordering involve placing higher-degree vertices earlier than lower-degree vertices, or choosing vertices with fewer available colors in preference to vertices that are less constrained. (Full article...)
Image 12

Hugo Steinhaus (1968)

Hugo Dyonizy Steinhaus (English: /ˈhjuːɡoʊ ˈstaɪnhaʊs/ HEW-goh STYNE-howss, Polish: [ˈxuɡɔ ˈʂtajnxaws], German: [ˈhuːɡoː ˈʃtaɪnhaʊs]; 14 January 1887 – 25 February 1972) was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the Jan Kazimierz University in Lwów (now Lviv, Ukraine), where he helped establish what later became known as the Lwów School of Mathematics. He is credited with "discovering" mathematician Stefan Banach, with whom he gave a notable contribution to functional analysis through the Banach–Steinhaus theorem. After World War II Steinhaus played an important part in the establishment of the mathematics department at Wrocław University and in the revival of Polish mathematics from the destruction of the war.

Author of around 170 scientific articles and books, Steinhaus has left his legacy and contribution in many branches of mathematics, such as functional analysis, geometry, mathematical logic, and trigonometry. Notably he is regarded as one of the early founders of game theory and probability theory, which led to later development of more comprehensive approaches by other scholars. (Full article...)

Did you know

... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?

Did you know...

...that it is impossible to devise a single formula involving only polynomials and radicals for solving an arbitrary quintic equation?
...that Euler found 59 more amicable numbers while for 2000 years, only 3 pairs had been found before him?
...that you cannot knot strings in 4 dimensions, but you can knot 2-dimensional surfaces, such as spheres?
...that there are 6 unsolved mathematics problems whose solutions will earn you one million US dollars each?
...that there are different sizes of infinite sets in set theory? More precisely, not all infinite cardinal numbers are equal?
...that every natural number can be written as the sum of four squares?
...that the largest known prime number is nearly 41 million digits long?

Featured pictures

Image 1Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
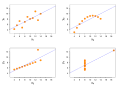
Image 31Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 33Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 33Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

Our website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.

Portal:Mathematics

Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.