Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Portal:Mathematics
-
Abacus, a ancient hand-operated calculating. -
Portrait of Emmy Noether, around 1900. -
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)
Featured articles
-
The weighing pans of this balance scale contain zero objects, divided into two equal groups.
In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...) -
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...) -
The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...) -
Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...) -
Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...) -
The manipulations of the Rubik's Cube form the Rubik's Cube group.
In mathematics, a group is a set with an operation that associates every pair of elements of the set to an element of the set (as does every binary operation) and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.
Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called (these properties characterize the integers in a unique way). (Full article...) -
Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...) -
Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...) -
Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...) -
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...) -
Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.
Archimedes' other mathematical achievements include deriving an approximation of pi (π), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...) -
Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.
In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...) -
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).
In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...) -
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.
In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
(Full article...) -
Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Good articles
-
In mathematics, the factorial of a non-negative integer , denoted by , is the product of all positive integers less than or equal to . The factorial of also equals the product of with the next smaller factorial:
For example,
The value of 0! is 1, according to the convention for an empty product.
Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book Sefer Yetzirah. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of distinct objects: there are . In mathematical analysis, factorials are used in power series for the exponential function and other functions, and they also have applications in algebra, number theory, probability theory, and computer science. (Full article...) -
The integer number line, a set of infinitely many points with integer distances. According to the Erdős–Anning theorem, any such set lies on a line.
The Erdős–Anning theorem states that, whenever an infinite number of points in the plane all have integer distances, the points lie on a straight line. The same result holds in higher dimensional Euclidean spaces.
The theorem cannot be strengthened to give a finite bound on the number of points: there exist arbitrarily large finite sets of points that are not on a line and have integer distances.
The theorem is named after Paul Erdős and Norman H. Anning, who published a proof of it in 1945. Erdős later supplied a simpler proof, which can also be used to check whether a point set forms an Erdős–Diophantine graph, an inextensible system of integer points with integer distances. The Erdős–Anning theorem inspired the Erdős–Ulam problem on the existence of dense point sets with rational distances. (Full article...) -
Using the Pythagorean theorem to compute two-dimensional Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance.
These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's Elements, distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. (Full article...) -
Fibonacci nim is played with a pile of coins. The number of coins in this pile, 21, is a Fibonacci number, so a game starting with this pile and played optimally will be won by the second player.
Fibonacci nim is a mathematical subtraction game, a variant of the game of nim. Players alternate removing coins from a pile, on each move taking at most twice as many coins as the previous move, and winning by taking the last coin. The Fibonacci numbers feature heavily in its analysis; in particular, the first player can win if and only if the starting number of coins is not a Fibonacci number. A complete strategy is known for best play in games with a single pile of counters, but not for variants of the game with multiple piles. (Full article...) -
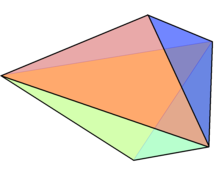
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid.
Many polyhedra are related to the triangular bipyramid, such as similar shapes derived from different approaches and the triangular prism as its dual polyhedron. Applications of a triangular bipyramid include trigonal bipyramidal molecular geometry which describes its atom cluster, a solution of the Thomson problem, and the representation of color order systems by the eighteenth century. (Full article...) -
Albert Einstein (/ˈaɪnstaɪn/, EYEN-styne; German: [ˈalbɛʁt ˈʔaɪnʃtaɪn] ⓘ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence formula E = mc2, which arises from special relativity, has been called "the world's most famous equation". He received the 1921 Nobel Prize in Physics forhis services to theoretical physics, and especially for his discovery of the law of the photoelectric effect
.
Born in the German Empire, Einstein moved to Switzerland in 1895, forsaking his German citizenship the following year. In 1897, at the age of seventeen, he enrolled in the mathematics and physics teaching diploma program at the Swiss Federal Polytechnic School in Zurich, graduating in 1900. He acquired Swiss citizenship a year later and afterwards secured a permanent position at the Swiss Patent Office in Bern. In 1905, he submitted a successful PhD dissertation to the University of Zurich. In 1914, he moved to Berlin to join the Prussian Academy of Sciences and the Humboldt University of Berlin, becoming director of the Kaiser Wilhelm Institute for Physics. In 1933, while Einstein was visiting the United States, Adolf Hitler came to power in Germany. Horrified by the Nazi persecution of his fellow Jews, he decided to remain in the US, and was granted American citizenship in 1940. On the eve of World War II, he endorsed a letter to President Franklin D. Roosevelt alerting him to the potential German nuclear weapons program and recommending that the US begin similar research. (Full article...) -
Francis Amasa Walker (July 2, 1840 – January 5, 1897) was an American economist, statistician, journalist, educator, academic administrator, and an officer in the Union Army.
Walker was born into a prominent Boston family, the son of the economist and politician Amasa Walker, and he graduated from Amherst College at the age of 20. He received a commission to join the 15th Massachusetts Infantry and quickly rose through the ranks as an assistant adjutant general. Walker fought in the Peninsula, Bristoe, Overland, and Richmond-Petersburg Campaigns before being captured by Confederate forces and held at the infamous Libby Prison. In July 1866, he was awarded the honorary grade of brevet brigadier general United States Volunteers, to rank from March 13, 1865, when he was 24 years old. (Full article...) -
16 polygonalizations of a set of six points
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.
Every point set that does not lie on a single line has at least one polygonalization, which can be found in polynomial time. For points in convex position, there is only one, but for some other point sets there can be exponentially many. Finding an optimal polygonalization under several natural optimization criteria is a hard problem, including as a special case the travelling salesman problem. The complexity of counting all polygonalizations remains unknown. (Full article...) -
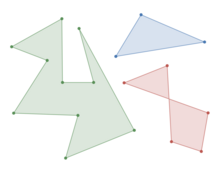
Two simple polygons (green and blue) and a self-intersecting polygon (red, in the lower right, not simple)
In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
The sum of external angles of a simple polygon is . Every simple polygon with sides can be triangulated by of its diagonals, and by the art gallery theorem its interior is visible from some of its vertices. (Full article...) -
Advanced Placement (AP) Statistics (also known as AP Stats) is a college-level high school statistics course offered in the United States through the College Board's Advanced Placement program. This course is equivalent to a one semester, non-calculus-based introductory college statistics course and is normally offered to sophomores, juniors and seniors in high school.
One of the College Board's more recent additions, the AP Statistics exam was first administered in May 1996 to supplement the AP program's math offerings, which had previously consisted of only AP Calculus AB and BC. In the United States, enrollment in AP Statistics classes has increased at a higher rate than in any other AP class. (Full article...) -
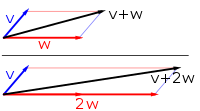
Vector addition and scalar multiplication: a vector v (blue) is added to another vector w (red, upper illustration). Below, w is stretched by a factor of 2, yielding the sum v + 2w.
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called vectors, can be added together and multiplied ("scaled") by numbers called scalars. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field.
Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities (such as forces and velocity) that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrices, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear equations. (Full article...) -
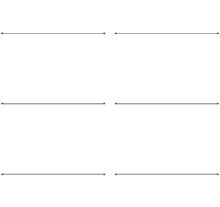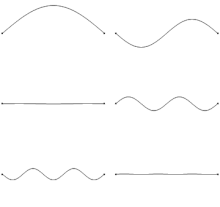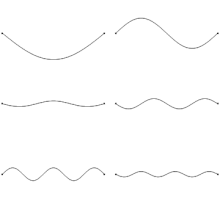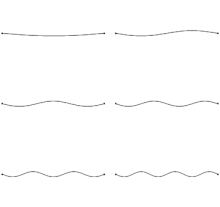
The state of a vibrating string can be modeled as a point in a Hilbert space. The decomposition of a vibrating string into its vibrations in distinct overtones is given by the projection of the point onto the coordinate axes in the space.
In mathematics, a Hilbert space (named for David Hilbert) generalizes the notion of Euclidean space. It extends the methods of linear algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is a vector space equipped with an inner product operation, which allows lengths and angles to be defined. Furthermore, Hilbert spaces are complete, which means that there are enough limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space.
Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term Hilbert space for the abstract concept that underlies many of these diverse applications. The success of Hilbert space methods ushered in a very fruitful era for functional analysis. Apart from the classical Euclidean vector spaces, examples of Hilbert spaces include spaces of square-integrable functions, spaces of sequences, Sobolev spaces consisting of generalized functions, and Hardy spaces of holomorphic functions. (Full article...)
Did you know
- ... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
- ... that people in Madagascar perform algebra on tree seeds in order to tell the future?
- ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
- ... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
- ... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
- ... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?
- ... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?
- ... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
- ... that, in the Rule 90 cellular automaton, any finite pattern eventually fills the whole array of cells with copies of itself?
- ... that, while the criss-cross algorithm visits all eight corners of the Klee–Minty cube when started at a worst corner, it visits only three more corners on average when started at a random corner?
- ...that in senary, all prime numbers other than 2 and 3 end in 1 or a 5?
- ...that, for all prime numbers p, the pth Perrin number is divisible by p?
- ...that it is impossible to trisect a general angle using only a ruler and a compass?
- ...that in a group of 23 people, there is a more than 50% chance that two people share a birthday?
- ...that the 1966 publication disproving Euler's sum of powers conjecture, proposed nearly 200 years earlier, consisted of only two sentences?
Featured pictures
-
Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics) -
Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
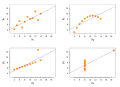
Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
-
Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
-
-
Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
-
-
-
-
-
Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
Get involved
- For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.
Categories
Topics
Index of articles
| ARTICLE INDEX: | |
| MATHEMATICIANS: |
Vital articles
- » subpages: Level 4 Mathematics articles, Level 5 Mathematics articles
Discover Wikipedia using portals
Previous Page Next Page
