Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
$Image 2 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 2
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 3
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 4
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)
Image 5

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
Image 6

A stamp of Zhang Heng issued by China Post in 1955

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
Image 7

Bust of Shen at the Beijing Ancient Observatory

Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
Image 8

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 9

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 10

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.

Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
Image 11
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 12
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group $S̃ 3$

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers ( $..., -2, -1, 0, 1, 2, ...$ ) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 13

One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.

Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
Image 14
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 15

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)

Good articles

Image 1
In this graph, the widest path from Maldon to Feering has bandwidth 29, and passes through Clacton, Tiptree, Harwich, and Blaxhall.

In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.

For instance, in a graph that represents connections between routers in the Internet, where the weight of an edge represents the bandwidth of a connection between two routers, the widest path problem is the problem of finding an end-to-end path between two Internet nodes that has the maximum possible bandwidth. The smallest edge weight on this path is known as the capacity or bandwidth of the path. As well as its applications in network routing, the widest path problem is also an important component of the Schulze method for deciding the winner of a multiway election, and has been applied to digital compositing, metabolic pathway analysis, and the computation of maximum flows. (Full article...)
Image 2
The brute force algorithm finds a 4-clique in this 7-vertex graph (the complement of the 7-vertex path graph) by systematically checking all C(7,4) = 35 4-vertex subgraphs for completeness.

In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size.

The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. (Full article...)
Image 3
17 indivisible camels

The 17-animal inheritance puzzle is a mathematical puzzle involving unequal but fair allocation of indivisible goods, usually stated in terms of inheritance of a number of large animals (17 camels, 17 horses, 17 elephants, etc.) which must be divided in some stated proportion among a number of beneficiaries. It is a common example of an apportionment problem.

Despite often being framed as a puzzle, it is more an anecdote about a curious calculation than a problem with a clear mathematical solution. Beyond recreational mathematics and mathematics education, the story has been repeated as a parable with varied metaphorical meanings. (Full article...)
Image 4

Einstein in 1921

Albert Einstein (/ˈaɪnstaɪn/, EYEN-styne; German: [ˈalbɛʁt ˈʔaɪnʃtaɪn] ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence formula E = mc2, which arises from special relativity, has been called "the world's most famous equation". He received the 1921 Nobel Prize in Physics for his services to theoretical physics, and especially for his discovery of the law of the photoelectric effect.

Born in the German Empire, Einstein moved to Switzerland in 1895, forsaking his German citizenship the following year. In 1897, at the age of seventeen, he enrolled in the mathematics and physics teaching diploma program at the Swiss Federal Polytechnic School in Zurich, graduating in 1900. He acquired Swiss citizenship a year later and afterwards secured a permanent position at the Swiss Patent Office in Bern. In 1905, he submitted a successful PhD dissertation to the University of Zurich. In 1914, he moved to Berlin to join the Prussian Academy of Sciences and the Humboldt University of Berlin, becoming director of the Kaiser Wilhelm Institute for Physics. In 1933, while Einstein was visiting the United States, Adolf Hitler came to power in Germany. Horrified by the Nazi persecution of his fellow Jews, he decided to remain in the US, and was granted American citizenship in 1940. On the eve of World War II, he endorsed a letter to President Franklin D. Roosevelt alerting him to the potential German nuclear weapons program and recommending that the US begin similar research. (Full article...)
Image 5
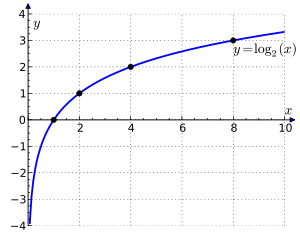
Graph of $log 2 x$ as a function of a positive real number $x$

In mathematics, the binary logarithm ( $log 2 n$ ) is the power to which the number $2$ must be raised to obtain the value $n$ . That is, for any real number $x$ ,
: $x=\log _{2}n\quad \Longleftrightarrow \quad 2^{x}=n.$
For example, the binary logarithm of $1$ is $0$ , the binary logarithm of $2$ is $1$ , the binary logarithm of $4$ is $2$ , and the binary logarithm of $32$ is $5$ .

The binary logarithm is the logarithm to the base $2$ and is the inverse function of the power of two function. There are several alternatives to the $log 2$ notation for the binary logarithm; see the Notation section below. (Full article...)
Image 6
The Petersen graph is the smallest snark.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

One of the equivalent forms of the four color theorem is that every snark is a non-planar graph. Research on snarks originated in Peter G. Tait's work on the four color theorem in 1880, but their name is much newer, given to them by Martin Gardner in 1976. Beyond coloring, snarks also have connections to other hard problems in graph theory: writing in the Electronic Journal of Combinatorics, Miroslav Chladný and Martin Škoviera state thatAs well as the problems they mention, W. T. Tutte's snark conjecture concerns the existence of Petersen graphs as graph minors of snarks; its proof has been long announced but remains unpublished, and would settle a special case of the existence of nowhere zero 4-flows. (Full article...)
Image 7
Thoralf Skolem, after whom the paradox is named

In mathematical logic and philosophy, Skolem's paradox is the apparent contradiction that a countable model of first-order set theory could contain an uncountable set. The paradox arises from part of the Löwenheim–Skolem theorem; Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as non-absoluteness. Although it is not an actual antinomy like Russell's paradox, the result is typically called a paradox and was described as a "paradoxical state of affairs" by Skolem.

In model theory, a model corresponds to a specific interpretation of a formal language or theory. It consists of a domain (a set of objects) and an interpretation of the symbols and formulas in the language, such that the axioms of the theory are satisfied within this structure. The Löwenheim–Skolem theorem shows that any model of set theory in first-order logic, if it is consistent, has an equivalent model that is countable. This appears contradictory, because Georg Cantor proved that there exist sets which are not countable. Thus the seeming contradiction is that a model that is itself countable, and which therefore contains only countable sets, satisfies the first-order sentence that intuitively states "there are uncountable sets". (Full article...)
Image 8
A 1-forest (a maximal pseudoforest), formed by three 1-trees

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.

The names are justified by analogy to the more commonly studied trees and forests. (A tree is a connected graph with no cycles; a forest is a disjoint union of trees.) Gabow and Tarjan attribute the study of pseudoforests to Dantzig's 1963 book on linear programming, in which pseudoforests arise in the solution of certain network flow problems. Pseudoforests also form graph-theoretic models of functions and occur in several algorithmic problems. Pseudoforests are sparse graphs – their number of edges is linearly bounded in terms of their number of vertices (in fact, they have at most as many edges as they have vertices) – and their matroid structure allows several other families of sparse graphs to be decomposed as unions of forests and pseudoforests. The name "pseudoforest" comes from Picard & Queyranne (1982). (Full article...)
Image 9
In mathematics, the three-gap theorem, three-distance theorem, or Steinhaus conjecture states that if one places $n$ points on a circle, at angles of $θ$ , $2 θ$ , $3 θ$ , ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two. Unless $θ$ is a rational multiple of $π$ , there will also be at least two distinct distances.

This result was conjectured by Hugo Steinhaus, and proved in the 1950s by Vera T. Sós, János Surányi [hu], and Stanisław Świerczkowski; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square. (Full article...)
Image 10
1 (one, unit, unity) is a number, numeral, and glyph. It is the first and smallest positive integer of the infinite sequence of natural numbers. This fundamental property has led to its unique uses in other fields, ranging from science to sports, where it commonly denotes the first, leading, or top thing in a group. 1 is the unit of counting or measurement, a determiner for singular nouns, and a gender-neutral pronoun. Historically, the representation of 1 evolved from ancient Sumerian and Babylonian symbols to the modern Arabic numeral.

In mathematics, 1 is the multiplicative identity, meaning that any number multiplied by 1 equals the same number. 1 is by convention not considered a prime number. In digital technology, 1 represents the "on" state in binary code, the foundation of computing. Philosophically, 1 symbolizes the ultimate reality or source of existence in various traditions. (Full article...)
Image 11

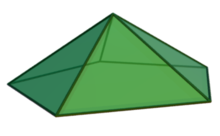
In geometry, a pentagonal pyramid is a pyramid with a pentagon base and five triangular faces, having a total of six faces. It is categorized as a Johnson solid if all of the edges are equal in length, forming equilateral triangular faces and a regular pentagonal base.

Pentagonal pyramids occur as pieces and tools in the construction of many polyhedra. They also appear in the field of natural science, as in stereochemistry where the shape can be described as the pentagonal pyramidal molecular geometry, as well as the study of shell assembling in the underlying potential energy surfaces and disclination in fivelings and related shapes such as pyramidal copper and other metal nanowires. (Full article...)
Image 12
A Möbius strip made with paper and adhesive tape

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.

As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve. (Full article...)

Did you know

... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
... that after Archimedes first defined convex curves, mathematicians lost interest in their analysis until the 19th century, more than two millennia later?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?

Did you know...

...that in a group of 23 people, there is a more than 50% chance that two people share a birthday?
...that the 1966 publication disproving Euler's sum of powers conjecture, proposed nearly 200 years earlier, consisted of only two sentences?
...the hyperbolic trigonometric functions of the natural logarithm can be represented by rational algebraic fractions?
... that economists blame market failures on non-convexity?
... that, according to the pizza theorem, a circular pizza that is sliced off-center into eight equal-angled wedges can still be divided equally between two people?
... that the clique problem of programming a computer to find complete subgraphs in an undirected graph was first studied as a way to find groups of people who all know each other in social networks?
... that the Herschel graph is the smallest possible polyhedral graph that does not have a Hamiltonian cycle?

Featured pictures

Image 1Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
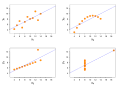
Image 28Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 31Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 31Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

Our website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.

Portal:Mathematics

Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.