Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Portal:Mathematics
-
Abacus, a ancient hand-operated calculating. -
Portrait of Emmy Noether, around 1900. -
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)
Featured articles
-
Logic studies valid forms of inference like modus ponens.
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like (and) or (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...) -
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.
In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
(Full article...) -
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃3
The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...) -
The manipulations of the Rubik's Cube form the Rubik's Cube group.
In mathematics, a group is a set with an operation that associates every pair of elements of the set to an element of the set (as does every binary operation) and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.
Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called (these properties characterize the integers in a unique way). (Full article...) -
Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...) -
Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...) -
The number π (/paɪ/ ⓘ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.
The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...) -
Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...) -
Theodore John Kaczynski (/kəˈzɪnski/ ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...) -
Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...) -
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...) -
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...) -
Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...) -
Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] ⓘ, Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.
Euler is credited for popularizing the Greek letter (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation for the value of a function, the letter to express the imaginary unit , the Greek letter (capital sigma) to express summations, the Greek letter (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...) -
Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
.jpg)
.jpg)
.jpg)
Good articles
-
Summa de arithmetica, geometria, proportioni et proportionalita (Summary of arithmetic, geometry, proportions and proportionality) is a book on mathematics written by Luca Pacioli and first published in 1494. It contains a comprehensive summary of Renaissance mathematics, including practical arithmetic, basic algebra, basic geometry and accounting, written for use as a textbook and reference work.
Written in vernacular Italian, the Summa is the first printed work on algebra, and it contains the first published description of the double-entry bookkeeping system. It set a new standard for writing and argumentation about algebra, and its impact upon the subsequent development and standardization of professional accounting methods was so great that Pacioli is sometimes referred to as the "father of accounting". (Full article...) -
In mathematics, a free abelian group is an abelian group with a basis. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis, also called an integral basis, is a subset such that every element of the group can be uniquely expressed as an integer combination of finitely many basis elements. For instance the two-dimensional integer lattice forms a free abelian group, with coordinatewise addition as its operation, and with the two points (1,0) and (0,1) as its basis. Free abelian groups have properties which make them similar to vector spaces, and may equivalently be called free -modules, the free modules over the integers. Lattice theory studies free abelian subgroups of real vector spaces. In algebraic topology, free abelian groups are used to define chain groups, and in algebraic geometry they are used to define divisors.
The elements of a free abelian group with basis may be described in several equivalent ways. These include formal sums over , which are expressions of the form where each is a nonzero integer, each is a distinct basis element, and the sum has finitely many terms. Alternatively, the elements of a free abelian group may be thought of as signed multisets containing finitely many elements of , with the multiplicity of an element in the multiset equal to its coefficient in the formal sum.
Another way to represent an element of a free abelian group is as a function from to the integers with finitely many nonzero values; for this functional representation, the group operation is the pointwise addition of functions. (Full article...) -
1 (one, unit, unity) is a number, numeral, and glyph. It is the first and smallest positive integer of the infinite sequence of natural numbers. This fundamental property has led to its unique uses in other fields, ranging from science to sports, where it commonly denotes the first, leading, or top thing in a group. 1 is the unit of counting or measurement, a determiner for singular nouns, and a gender-neutral pronoun. Historically, the representation of 1 evolved from ancient Sumerian and Babylonian symbols to the modern Arabic numeral.
In mathematics, 1 is the multiplicative identity, meaning that any number multiplied by 1 equals the same number. 1 is by convention not considered a prime number. In digital technology, 1 represents the "on" state in binary code, the foundation of computing. Philosophically, 1 symbolizes the ultimate reality or source of existence in various traditions. (Full article...) -
Georg Cantor, c. 1870
Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties. One of these theorems is his "revolutionary discovery" that the set of all real numbers is uncountably, rather than countably, infinite. This theorem is proved using Cantor's first uncountability proof, which differs from the more familiar proof using his diagonal argument. The title of the article, "On a Property of the Collection of All Real Algebraic Numbers" ("Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen"), refers to its first theorem: the set of real algebraic numbers is countable. Cantor's article was published in 1874. In 1879, he modified his uncountability proof by using the topological notion of a set being dense in an interval.
Cantor's article also contains a proof of the existence of transcendental numbers. Both constructive and non-constructive proofs have been presented as "Cantor's proof." The popularity of presenting a non-constructive proof has led to a misconception that Cantor's arguments are non-constructive. Since the proof that Cantor published either constructs transcendental numbers or does not, an analysis of his article can determine whether or not this proof is constructive. Cantor's correspondence with Richard Dedekind shows the development of his ideas and reveals that he had a choice between two proofs: a non-constructive proof that uses the uncountability of the real numbers and a constructive proof that does not use uncountability. (Full article...) -
Two random distributions on three-vertex binary trees, the binary search trees on three keys a, b, and c. These five trees are each assigned probability 1/5 by the uniform distribution (top). The distribution generated by random insertion orderings (bottom) assigns the center tree probability 1/3, because two of the six possible insertion orderings generate the same tree; the other four trees have probability 1/6.
In computer science and probability theory, a random binary tree is a binary tree selected at random from some probability distribution on binary trees. Different distributions have been used, leading to different properties for these trees.
Random binary trees have been used for analyzing the average-case complexity of data structures based on binary search trees. For this application it is common to use random trees formed by inserting nodes one at a time according to a random permutation. The resulting trees are very likely to have logarithmic depth and logarithmic Strahler number. The treap and related balanced binary search trees use update operations that maintain this random structure even when the update sequence is non-random. (Full article...) -
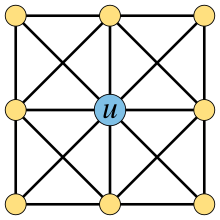
A graph with a universal vertex, u
In graph theory, a universal vertex is a vertex of an undirected graph that is adjacent to all other vertices of the graph. It may also be called a dominating vertex, as it forms a one-element dominating set in the graph. A graph that contains a universal vertex may be called a cone, and its universal vertex may be called the apex of the cone. This terminology should be distinguished from the unrelated usage of these words for universal quantifiers in the logic of graphs, and for apex graphs.
Graphs that contain a universal vertex include the stars, trivially perfect graphs, and friendship graphs. For wheel graphs (the graphs of pyramids), and graphs of higher-dimensional pyramidal polytopes, the vertex at the apex of the pyramid is universal. When a graph contains a universal vertex, it is a cop-win graph, and almost all cop-win graphs contain a universal vertex. (Full article...) -
Vojtěch Jarník (Czech pronunciation: [ˈvojcɛx ˈjarɲiːk]; 22 December 1897 – 22 September 1970) was a Czech mathematician. He worked for many years as a professor and administrator at Charles University, and helped found the Czechoslovak Academy of Sciences. He is the namesake of Jarník's algorithm for minimum spanning trees.
Jarník worked in number theory, mathematical analysis, and graph algorithms. He has been called "probably the first Czechoslovak mathematician whose scientific works received wide and lasting international response". As well as developing Jarník's algorithm, he found tight bounds on the number of lattice points on convex curves, studied the relationship between the Hausdorff dimension of sets of real numbers and how well they can be approximated by rational numbers, and investigated the properties of nowhere-differentiable functions. (Full article...) -
A perspective projection of a dodecahedral tessellation in H3. Note the recursive structure: each pentagon contains smaller pentagons, which contain smaller pentagons. This is an example of a subdivision rule arising from a finite universe (i.e. a closed 3-manifold).
In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals. Subdivision rules have been used in architecture, biology, and computer science, as well as in the study of hyperbolic manifolds. Substitution tilings are a well-studied type of subdivision rule. (Full article...) -
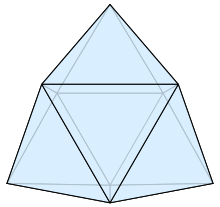
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.
The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle. (Full article...) -
The regular heptagon cannot be constructed using only a straightedge and compass construction; this can be proven using the field of constructible numbers.
In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and p-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many elements. (Full article...) -
Graphical demonstration that 1 = 1/2 + 1/3 + 1/11 + 1/23 + 1/31 + 1/(2×3×11×23×31). Each row of k squares of side length 1/k has total area 1/k, and all the squares together exactly cover a larger square with area 1. The bottom row of 47058 squares with side length 1/47058 is too small to see in the figure and is not shown.
In number theory, Znám's problem asks which sets of integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other mathematicians had considered similar problems around the same time.
The initial terms of Sylvester's sequence almost solve this problem, except that the last chosen term equals one plus the product of the others, rather than being a proper divisor. Sun (1983) showed that there is at least one solution to the (proper) Znám problem for each . Sun's solution is based on a recurrence similar to that for Sylvester's sequence, but with a different set of initial values. (Full article...) -
In number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1. Wieferich primes were first described by Arthur Wieferich in 1909 in works pertaining to Fermat's Last Theorem, at which time both of Fermat's theorems were already well known to mathematicians.
Since then, connections between Wieferich primes and various other topics in mathematics have been discovered, including other types of numbers and primes, such as Mersenne and Fermat numbers, specific types of pseudoprimes and some types of numbers generalized from the original definition of a Wieferich prime. Over time, those connections discovered have extended to cover more properties of certain prime numbers as well as more general subjects such as number fields and the abc conjecture. (Full article...)
.svg)
Did you know
- ... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
- ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
- ... that multiple mathematics competitions have made use of Sophie Germain's identity?
- ... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
- ... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
- ... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
- ... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
- ... that ten-sided gaming dice have kite-shaped faces?
- ...that the six permutations of the vector (1,2,3) form a regular hexagon in 3d space, the 24 permutations of (1,2,3,4) form a truncated octahedron in four dimensions, and both are examples of permutohedra?
- ...that Ostomachion is a mathematical treatise attributed to Archimedes on a 14-piece tiling puzzle similar to tangram?
- ...that some functions can be written as an infinite sum of trigonometric polynomials and that this sum is called the Fourier series of that function?
- ...that the identity elements for arithmetic operations make use of the only two whole numbers that are neither composites nor prime numbers, 0 and 1?
- ...that as of April 2010 only 35 even numbers have been found that are not the sum of two primes which are each in a Twin Primes pair? ref
- ...the Piphilology record (memorizing digits of Pi) is 70000 as of Mar 2015?
- ...that people are significantly slower to identify the parity of zero than other whole numbers, regardless of age, language spoken, or whether the symbol or word for zero is used?
Featured pictures
-
-
-
-
-
-
-
Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics) -
Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics) -
Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
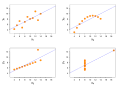
Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
-
-
-
-
-
-
-
-
Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
-
-
Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics) -
-
-
Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics) -
Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Get involved
- For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.
Categories
Topics
Index of articles
| ARTICLE INDEX: | |
| MATHEMATICIANS: |
Vital articles
- » subpages: Level 4 Mathematics articles, Level 5 Mathematics articles
Discover Wikipedia using portals
Previous Page Next Page
