Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 2
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 3
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group $S̃ 3$

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers ( $..., -2, -1, 0, 1, 2, ...$ ) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 4

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 5
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.

Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
Image 6
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 7

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 8

Archimedes Thoughtful by Fetti (1620)

Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

Archimedes' other mathematical achievements include deriving an approximation of pi ( $π$ ), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
Image 9

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
Image 10

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
Image 11

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 12

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.

Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
Image 13
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
Image 14

A stamp of Zhang Heng issued by China Post in 1955

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
Image 15

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)

Good articles

Image 1
Vedic Mathematics is a book written by Indian Shankaracharya Bharati Krishna Tirtha and first published in 1965. It contains a list of mathematical techniques which were falsely claimed to contain advanced mathematical knowledge. The book was posthumously published under its deceptive title by editor V. S. Agrawala, who noted in the foreword that the claim of Vedic origin, made by the original author and implied by the title, was unsupported.

Neither Krishna Tirtha nor Agrawala were able to produce sources, and scholars unanimously note it to be a compendium of methods for increasing the speed of elementary mathematical calculations sharing no overlap with historical mathematical developments during the Vedic period. Nonetheless, there has been a proliferation of publications in this area and multiple attempts to integrate the subject into mainstream education at the state level by right-wing Hindu nationalist governments. (Full article...)
Image 2
Rule 184, run for 128 steps from random configurations with each of three different starting densities: top 25%, middle 50%, bottom 75%. The view shown is a 300-pixel crop from a wider simulation.

Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:
- Rule 184 can be used as a simple model for traffic flow in a single lane of a highway, and forms the basis for many cellular automaton models of traffic flow with greater sophistication. In this model, particles (representing vehicles) move in a single direction, stopping and starting depending on the cars in front of them. The number of particles remains unchanged throughout the simulation. Because of this application, Rule 184 is sometimes called the "traffic rule".
- Rule 184 also models a form of deposition of particles onto an irregular surface, in which each local minimum of the surface is filled with a particle in each step. At each step of the simulation, the number of particles increases. Once placed, a particle never moves.
- Rule 184 can be understood in terms of ballistic annihilation, a system of particles moving both leftwards and rightwards through a one-dimensional medium. When two such particles collide, they annihilate each other, so that at each step the number of particles remains unchanged or decreases.
The apparent contradiction between these descriptions is resolved by different ways of associating features of the automaton's state with particles. (Full article...)
Image 3
An antiparallelogram

In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, each pair of sides is antiparallel with respect to the other, with sides in the longer pair crossing each other as in a scissors mechanism. Whereas a parallelogram's opposite angles are equal and oriented the same way, an antiparallelogram's are equal but oppositely oriented. Antiparallelograms are also called contraparallelograms or crossed parallelograms.

Antiparallelograms occur as the vertex figures of certain nonconvex uniform polyhedra. In the theory of four-bar linkages, the linkages with the form of an antiparallelogram are also called butterfly linkages or bow-tie linkages, and are used in the design of non-circular gears. In celestial mechanics, they occur in certain families of solutions to the 4-body problem. (Full article...)
Image 4
A binary tiling in the Poincaré disk model of the hyperbolic plane. Each tile edge lies on a horocycle (shown as circles interior to the disk) or a hyperbolic line (arcs perpendicular to the disk boundary). The horocycles and lines are asymptotic to an ideal point located at the right side of the Poincaré disk.

In geometry, a binary tiling (sometimes called a Böröczky tiling) is a tiling of the hyperbolic plane, resembling a quadtree over the Poincaré half-plane model of the hyperbolic plane. The tiles are congruent, each adjoining five others. They may be convex pentagons, or non-convex shapes with four sides, alternatingly line segments and horocyclic arcs, meeting at four right angles.

There are uncountably many distinct binary tilings for a given shape of tile. They are all weakly aperiodic, which means that they can have a one-dimensional symmetry group but not a two-dimensional family of symmetries. There exist binary tilings with tiles of arbitrarily small area. (Full article...)
Image 5
The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex.

A Reuleaux triangle [ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

They are named after Franz Reuleaux, a 19th-century German engineer who pioneered the study of machines for translating one type of motion into another, and who used Reuleaux triangles in his designs. However, these shapes were known before his time, for instance by the designers of Gothic church windows, by Leonardo da Vinci, who used it for a map projection, and by Leonhard Euler in his study of constant-width shapes. Other applications of the Reuleaux triangle include giving the shape to guitar picks, fire hydrant nuts, pencils, and drill bits for drilling filleted square holes, as well as in graphic design in the shapes of some signs and corporate logos. (Full article...)
Image 6

L6a4

In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.

The Borromean rings are named after the Italian House of Borromeo, who used the circular form of these rings as an element of their coat of arms, but designs based on the Borromean rings have been used in many cultures, including by the Norsemen and in Japan. They have been used in Christian symbolism as a sign of the Trinity, and in modern commerce as the logo of Ballantine beer, giving them the alternative name Ballantine rings. Physical instances of the Borromean rings have been made from linked DNA or other molecules, and they have analogues in the Efimov state and Borromean nuclei, both of which have three components bound to each other although no two of them are bound. (Full article...)
Image 7

1963 statue of Anania Shirakatsi holding a globe at the entrance of the Matenadaran

Anania Shirakatsi (Old Armenian: Անանիա Շիրակացի, Anania Širakac’i, anglicized: Ananias of Shirak) was a 7th-century Armenian polymath and natural philosopher, author of extant works covering mathematics, astronomy, geography, chronology, and other fields. Little is known for certain of his life outside of his own writings, but he is considered the father of the exact and natural sciences in Armenia—the first Armenian mathematician, astronomer, and cosmographer.

A part of the Armenian Hellenizing School and one of the few secular scholars in medieval Armenia, Anania was educated primarily by Tychicus, in Trebizond. He composed science textbooks and the first known geographic work in classical Armenian (Ashkharhatsuyts), which provides detailed information about Greater Armenia, Persia and the Caucasus (Georgia and Caucasian Albania). (Full article...)
Image 8
A set of 20 points in a 10 × 10 grid, with no three points in a line.

The no-three-in-line problem in discrete geometry asks how many points can be placed in the $n\times n$ grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".

At most $2n$ points can be placed, because $2n+1$ points in a grid would include a row of three or more points, by the pigeonhole principle. Although the problem can be solved with $2n$ points for every $n$ up to $46$ , it is conjectured that fewer than $2n$ points can be placed in grids of large size. Known methods can place linearly many points in grids of arbitrary size, but the best of these methods place slightly fewer than $1.5n$ points, not $2n$ . (Full article...)
Image 9
A polyhedron and its midsphere. The red circles are the boundaries of spherical caps within which the surface of the sphere can be seen from each vertex.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals (Catalan solids) all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

When a polyhedron has a midsphere, one can form two perpendicular circle packings on the midsphere, one corresponding to the adjacencies between vertices of the polyhedron, and the other corresponding in the same way to its polar polyhedron, which has the same midsphere. The length of each polyhedron edge is the sum of the distances from its two endpoints to their corresponding circles in this circle packing. (Full article...)
Image 10
Wave functions of the electron in a hydrogen atom at different energy levels. Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations. The brighter areas represent a higher probability of finding the electron.

Quantum mechanics is a fundamental theory that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.

Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation, valid at large (macroscopic/microscopic) scale. (Full article...)
$Image 11 The main arithmetic operations are addition, subtraction, multiplication, and division. Arithmetic is an elementary branch of mathematics that studies numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms. Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. (Full article...)$

Image 11
The main arithmetic operations are addition, subtraction, multiplication, and division.

Arithmetic is an elementary branch of mathematics that studies numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.

Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. (Full article...)
Image 12
Ronald Paul "Ron" Fedkiw (born February 27, 1968) is a full professor in the Stanford University department of computer science and a leading researcher in the field of computer graphics, focusing on topics relating to physically based simulation of natural phenomena and machine learning. His techniques have been employed in many motion pictures. He has earned recognition at the 80th Academy Awards and the 87th Academy Awards as well as from the National Academy of Sciences.

His first Academy Award was awarded for developing techniques that enabled many technically sophisticated adaptations including the visual effects in 21st century movies in the Star Wars, Harry Potter, Terminator, and Pirates of the Caribbean franchises. Fedkiw has designed a platform that has been used to create many of the movie world's most advanced special effects since it was first used on the T-X character in Terminator 3: Rise of the Machines. His second Academy Award was awarded for computer graphics techniques for special effects for large scale destruction. Although he has won an Oscar for his work, he does not design the visual effects that use his technique. Instead, he has developed a system that other award-winning technicians and engineers have used to create visual effects for some of the world's most expensive and highest-grossing movies. (Full article...)

Did you know

... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
... that multiple mathematics competitions have made use of Sophie Germain's identity?

Did you know...

...that the 1966 publication disproving Euler's sum of powers conjecture, proposed nearly 200 years earlier, consisted of only two sentences?
...the hyperbolic trigonometric functions of the natural logarithm can be represented by rational algebraic fractions?
... that economists blame market failures on non-convexity?
... that, according to the pizza theorem, a circular pizza that is sliced off-center into eight equal-angled wedges can still be divided equally between two people?
... that the clique problem of programming a computer to find complete subgraphs in an undirected graph was first studied as a way to find groups of people who all know each other in social networks?
... that the Herschel graph is the smallest possible polyhedral graph that does not have a Hamiltonian cycle?
... that the Life without Death cellular automaton, a mathematical model of pattern formation, is a variant of Conway's Game of Life in which cells, once brought to life, never die?

Featured pictures

Image 1Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
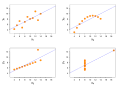
Image 27Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 30Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 30Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

Our website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.

Portal:Mathematics

Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.