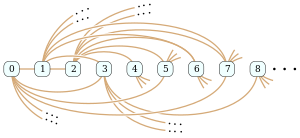Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 2
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 3
Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
Image 4
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group $S̃ 3$

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers ( $..., -2, -1, 0, 1, 2, ...$ ) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 5
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 6

The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.

In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
Image 7

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.

Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
Image 8
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 9

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 10

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 11

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 12
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 13
The manipulations of the Rubik's Cube form the Rubik's Cube group.

In mathematics, a group is a set with an operation that associates every pair of elements of the set to an element of the set (as does every binary operation) and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.

Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠ $1$ ⁠ (these properties characterize the integers in a unique way). (Full article...)
Image 14

Archimedes Thoughtful by Fetti (1620)

Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

Archimedes' other mathematical achievements include deriving an approximation of pi ( $π$ ), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
Image 15

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)

Good articles

Image 1
Vojtěch Jarník (Czech pronunciation: [ˈvojcɛx ˈjarɲiːk]; 22 December 1897 – 22 September 1970) was a Czech mathematician. He worked for many years as a professor and administrator at Charles University, and helped found the Czechoslovak Academy of Sciences. He is the namesake of Jarník's algorithm for minimum spanning trees.

Jarník worked in number theory, mathematical analysis, and graph algorithms. He has been called "probably the first Czechoslovak mathematician whose scientific works received wide and lasting international response". As well as developing Jarník's algorithm, he found tight bounds on the number of lattice points on convex curves, studied the relationship between the Hausdorff dimension of sets of real numbers and how well they can be approximated by rational numbers, and investigated the properties of nowhere-differentiable functions. (Full article...)
Image 2
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.

In technical terms, QED can be described as a very accurate way to calculate the probability of the position and movement of particles, even those massless such as photons, and the quantity depending on position (field) of those particles, and described light and matter beyond the wave-particle duality proposed by Albert Einstein in 1905. Richard Feynman called it "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen. It is the most precise and stringently tested theory in physics. (Full article...)
Image 3
In this example, the alternating sum of angles (clockwise from the bottom) is 90° − 45° + 22.5° − 22.5° + 45° − 90° + 22.5° − 22.5° = 0°. Since it adds to zero, the crease pattern may be flat-folded.

Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero.
Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.

The theorem is named after one of its discoverers, Toshikazu Kawasaki. However, several others also contributed to its discovery, and it is sometimes called the Kawasaki–Justin theorem or Husimi's theorem after other contributors, Jacques Justin and Kôdi Husimi. (Full article...)
Image 4
Fermat's Last Tango is a 2000 off-Broadway musical about the proof of Fermat's Last Theorem, written by husband and wife Joshua Rosenblum (music, lyrics) and Joanne Sydney Lessner (book, lyrics). The musical presents a fictionalized version of the real life story of Andrew Wiles, and has been praised for the accuracy of the mathematical content. The original production at the York Theatre received mixed reviews, but the musical was well received by mathematical audiences. A video of the original production has been distributed by the Clay Mathematics Institute and shown at several mathematical conferences and similar occasions. The musical has also been translated into Portuguese. (Full article...)
Image 5
Ronald Paul "Ron" Fedkiw (born February 27, 1968) is a full professor in the Stanford University department of computer science and a leading researcher in the field of computer graphics, focusing on topics relating to physically based simulation of natural phenomena and machine learning. His techniques have been employed in many motion pictures. He has earned recognition at the 80th Academy Awards and the 87th Academy Awards as well as from the National Academy of Sciences.

His first Academy Award was awarded for developing techniques that enabled many technically sophisticated adaptations including the visual effects in 21st century movies in the Star Wars, Harry Potter, Terminator, and Pirates of the Caribbean franchises. Fedkiw has designed a platform that has been used to create many of the movie world's most advanced special effects since it was first used on the T-X character in Terminator 3: Rise of the Machines. His second Academy Award was awarded for computer graphics techniques for special effects for large scale destruction. Although he has won an Oscar for his work, he does not design the visual effects that use his technique. Instead, he has developed a system that other award-winning technicians and engineers have used to create visual effects for some of the world's most expensive and highest-grossing movies. (Full article...)
Image 6
In graph theory, a cop-win graph is an undirected graph on which the pursuer (cop) can always win a pursuit–evasion game against a robber, with the players taking alternating turns in which they can choose to move along an edge of a graph or stay put, until the cop lands on the robber's vertex. Finite cop-win graphs are also called dismantlable graphs or constructible graphs, because they can be dismantled by repeatedly removing a dominated vertex (one whose closed neighborhood is a subset of another vertex's neighborhood) or constructed by repeatedly adding such a vertex. The cop-win graphs can be recognized in polynomial time by a greedy algorithm that constructs a dismantling order. They include the chordal graphs, and the graphs that contain a universal vertex. (Full article...)
Image 7
Paterson's worms are a family of cellular automata devised in 1971 by Mike Paterson and John Horton Conway to model the behaviour and feeding patterns of certain prehistoric worms. In the model, a worm moves between points on a triangular grid along line segments, representing food. Its turnings are determined by the configuration of eaten and uneaten line segments adjacent to the point at which the worm currently is. Despite being governed by simple rules the behaviour of the worms can be extremely complex, and the ultimate fate of one variant is still unknown.

The worms were studied in the early 1970s by Paterson, Conway and Michael Beeler, described by Beeler in June 1973, and presented in November 1973 in Martin Gardner's "Mathematical Games" column in Scientific American. (Full article...)
Image 8

Bust of Pythagoras of Samos in the
Capitoline Museums, Rome

Pythagoras of Samos (Ancient Greek: Πυθαγόρας; c. 570 – c. 495 BC) was an ancient Ionian Greek philosopher, polymath, and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, the West in general. Knowledge of his life is clouded by legend; modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, ascetic lifestyle.

In antiquity, Pythagoras was credited with many mathematical and scientific discoveries, including the Pythagorean theorem, Pythagorean tuning, the five regular solids, the Theory of Proportions, the sphericity of the Earth, and the identity of the morning and evening stars as the planet Venus. It was said that he was the first man to call himself a philosopher ("lover of wisdom") and that he was the first to divide the globe into five climatic zones. Classical historians debate whether Pythagoras made these discoveries, and many of the accomplishments credited to him likely originated earlier or were made by his colleagues or successors. Some accounts mention that the philosophy associated with Pythagoras was related to mathematics and that numbers were important, but it is debated to what extent, if at all, he actually contributed to mathematics or natural philosophy. (Full article...)
Image 9
In mathematics, the three-gap theorem, three-distance theorem, or Steinhaus conjecture states that if one places $n$ points on a circle, at angles of $θ$ , $2 θ$ , $3 θ$ , ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two. Unless $θ$ is a rational multiple of $π$ , there will also be at least two distinct distances.

This result was conjectured by Hugo Steinhaus, and proved in the 1950s by Vera T. Sós, János Surányi [hu], and Stanisław Świerczkowski; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square. (Full article...)
Image 10
Four opaque sets for a unit square. Upper left: its boundary, length 4. Upper right: Three sides, length 3. Lower left: a Steiner tree of the vertices, length $1+{\sqrt {3}}\approx 2.732$ . Lower right: the conjectured optimal solution, length ${\sqrt {2}}+{\tfrac {1}{2}}{\sqrt {6}}\approx 2.639$ .

In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or (in cases where they have the form of a forest of line segments or other curves) opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.

For instance, visibility through a unit square can be blocked by its four boundary edges, with length 4, but a shorter opaque forest blocks visibility across the square with length ${\sqrt {2}}+{\tfrac {1}{2}}{\sqrt {6}}\approx 2.639$ . It is unproven whether this is the shortest possible opaque set for the square, and for most other shapes this problem similarly remains unsolved. The shortest opaque set for any bounded convex set in the plane has length at most the perimeter of the set, and at least half the perimeter. For the square, a slightly stronger lower bound than half the perimeter is known. Another convex set whose opaque sets are commonly studied is the unit circle, for which the shortest connected opaque set has length $2+\pi$ . Without the assumption of connectivity, the shortest opaque set for the circle has length at least $\pi$ and at most $4.7998$ . (Full article...)
Image 11
A Hasse diagram of divisibility relationships among the regular numbers up to 400. The vertical scale is logarithmic.

Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 60² = 3600 = 48 × 75, so as divisors of a power of 60 both 48 and 75 are regular.

These numbers arise in several areas of mathematics and its applications, and have different names coming from their different areas of study.
- In number theory, these numbers are called 5-smooth, because they can be characterized as having only 2, 3, or 5 as their prime factors. This is a specific case of the more general $k$ -smooth numbers, the numbers that have no prime factor greater than $k$ .* In the study of Babylonian mathematics, the divisors of powers of 60 are called regular numbers or regular sexagesimal numbers, and are of great importance in this area because of the sexagesimal (base 60) number system that the Babylonians used for writing their numbers, and that was central to Babylonian mathematics.
- In music theory, regular numbers occur in the ratios of tones in five-limit just intonation. In connection with music theory and related theories of architecture, these numbers have been called the harmonic whole numbers.
- In computer science, regular numbers are often called Hamming numbers, after Richard Hamming, who proposed the problem of finding computer algorithms for generating these numbers in ascending order. This problem has been used as a test case for functional programming.
(Full article...)
Image 12
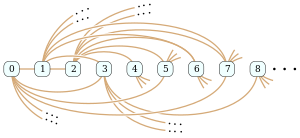
The Rado graph, as numbered by Ackermann (1937) and Rado (1964).

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed (with probability one) by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann (1937). The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

Every finite or countably infinite graph is an induced subgraph of the Rado graph, and can be found as an induced subgraph by a greedy algorithm that builds up the subgraph one vertex at a time. The Rado graph is uniquely defined, among countable graphs, by an extension property that guarantees the correctness of this algorithm: no matter which vertices have already been chosen to form part of the induced subgraph, and no matter what pattern of adjacencies is needed to extend the subgraph by one more vertex, there will always exist another vertex with that pattern of adjacencies that the greedy algorithm can choose. (Full article...)

Did you know

... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?
... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
... that ten-sided gaming dice have kite-shaped faces?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?

Did you know...

... that, according to the pizza theorem, a circular pizza that is sliced off-center into eight equal-angled wedges can still be divided equally between two people?
... that the clique problem of programming a computer to find complete subgraphs in an undirected graph was first studied as a way to find groups of people who all know each other in social networks?
... that the Herschel graph is the smallest possible polyhedral graph that does not have a Hamiltonian cycle?
... that the Life without Death cellular automaton, a mathematical model of pattern formation, is a variant of Conway's Game of Life in which cells, once brought to life, never die?
... that one can list every positive rational number without repetition by breadth-first traversal of the Calkin–Wilf tree?
... that the Hadwiger conjecture implies that the external surface of any three-dimensional convex body can be illuminated by only eight light sources, but the best proven bound is that 16 lights are sufficient?
... that an equitable coloring of a graph, in which the numbers of vertices of each color are as nearly equal as possible, may require far more colors than a graph coloring without this constraint?

Featured pictures

Image 1Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
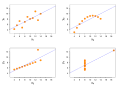
Image 14Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 15Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 15Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

Our website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.

Portal:Mathematics

Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.