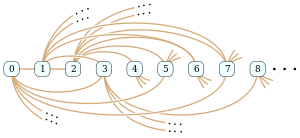Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.

Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
Image 2

Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
Image 3
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 4

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 5
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 6
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 7
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 8

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
Image 9
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 10
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 11

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 12

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.

Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
Image 13
Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
$Image 14 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 14
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 15

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)

Good articles

Image 1
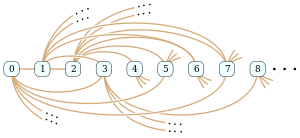
The Rado graph, as numbered by Ackermann (1937) and Rado (1964).

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed (with probability one) by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann (1937). The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

Every finite or countably infinite graph is an induced subgraph of the Rado graph, and can be found as an induced subgraph by a greedy algorithm that builds up the subgraph one vertex at a time. The Rado graph is uniquely defined, among countable graphs, by an extension property that guarantees the correctness of this algorithm: no matter which vertices have already been chosen to form part of the induced subgraph, and no matter what pattern of adjacencies is needed to extend the subgraph by one more vertex, there will always exist another vertex with that pattern of adjacencies that the greedy algorithm can choose. (Full article...)
Image 2

von Neumann in the 1940s

John von Neumann (/vɒn ˈnɔɪmən/ von NOY-mən; Hungarian: Neumann János Lajos [ˈnɒjmɒn ˈjaːnoʃ ˈlɒjoʃ]; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, integrating pure and applied sciences and making major contributions to many fields, including mathematics, physics, economics, computing, and statistics. He was a pioneer in building the mathematical framework of quantum physics, in the development of functional analysis, and in game theory, introducing or codifying concepts including cellular automata, the universal constructor and the digital computer. His analysis of the structure of self-replication preceded the discovery of the structure of DNA.

During World War II, von Neumann worked on the Manhattan Project. He developed the mathematical models behind the explosive lenses used in the implosion-type nuclear weapon. Before and after the war, he consulted for many organizations including the Office of Scientific Research and Development, the Army's Ballistic Research Laboratory, the Armed Forces Special Weapons Project and the Oak Ridge National Laboratory. At the peak of his influence in the 1950s, he chaired a number of Defense Department committees including the Strategic Missile Evaluation Committee and the ICBM Scientific Advisory Committee. He was also a member of the influential Atomic Energy Commission in charge of all atomic energy development in the country. He played a key role alongside Bernard Schriever and Trevor Gardner in the design and development of the United States' first ICBM programs. At that time he was considered the nation's foremost expert on nuclear weaponry and the leading defense scientist at the U.S. Department of Defense. (Full article...)
$Image 3 "The Gherkin", 30 St Mary Axe, London, completed 2003, is a parametrically designed solid of revolution. Mathematics and architecture are related, since architecture, like some other arts, uses mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create architectural forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings. In ancient Egypt, ancient Greece, India, and the Islamic world, buildings including pyramids, temples, mosques, palaces and mausoleums were laid out with specific proportions for religious reasons. In Islamic architecture, geometric shapes and geometric tiling patterns are used to decorate buildings, both inside and outside. Some Hindu temples have a fractal-like structure where parts resemble the whole, conveying a message about the infinite in Hindu cosmology. In Chinese architecture, the tulou of Fujian province are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings. (Full article...)$

Image 3
"The Gherkin", 30 St Mary Axe, London, completed 2003, is a parametrically designed solid of revolution.

Mathematics and architecture are related, since architecture, like some other arts, uses mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create architectural forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings.

In ancient Egypt, ancient Greece, India, and the Islamic world, buildings including pyramids, temples, mosques, palaces and mausoleums were laid out with specific proportions for religious reasons. In Islamic architecture, geometric shapes and geometric tiling patterns are used to decorate buildings, both inside and outside. Some Hindu temples have a fractal-like structure where parts resemble the whole, conveying a message about the infinite in Hindu cosmology. In Chinese architecture, the tulou of Fujian province are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings. (Full article...)
Image 4
Walton in Pomona College's Walker Lounge c. 1957

Jean Brosius Walton (March 6, 1914 – July 5, 2006) was an American academic administrator and women's studies scholar. She spent the bulk of her career at Pomona College in Claremont, California.

Born to a Pennsylvania Quaker family, Walton grew up at George School and studied mathematics at Swarthmore College, Brown University and the University of Pennsylvania. She joined Pomona College in 1949 as the Dean of Women, and was promoted to dean of students in 1969 and vice president for student affairs in 1976, three years before her formal retirement. During her tenure, she advocated for women's education, engaged with student protests against the Vietnam War, oversaw reform of residential life policies to eliminate parietal rules, and co-founded the Claremont Colleges' Intercollegiate Women's Studies Program. She earned widespread recognition for her work and was praised by colleagues for her independent and dignified personality. (Full article...)
Image 5
The small set expansion hypothesis or small set expansion conjecture in computational complexity theory is an unproven computational hardness assumption. Under the small set expansion hypothesis it is assumed to be computationally infeasible to distinguish between a certain class of expander graphs called "small set expanders" and other graphs that are very far from being small set expanders. This assumption implies the hardness of several other computational problems, and the optimality of certain known approximation algorithms.

The small set expansion hypothesis is related to the unique games conjecture, another unproven computational hardness assumption according to which accurately approximating the value of certain games is computationally infeasible. If the small set expansion hypothesis is true, then so is the unique games conjecture. (Full article...)
Image 6
Hypatia (born c. 350–370 - March 415 AD) was a Neoplatonist philosopher, astronomer, and mathematician who lived in Alexandria, Egypt, then part of the Eastern Roman Empire. She was a prominent thinker in Alexandria where she taught philosophy and astronomy. Although preceded by Pandrosion, another Alexandrian female mathematician, she is the first female mathematician whose life is reasonably well recorded. Hypatia was renowned in her own lifetime as a great teacher and a wise counselor. She wrote a commentary on Diophantus's thirteen-volume Arithmetica, which may survive in part, having been interpolated into Diophantus's original text, and another commentary on Apollonius of Perga's treatise on conic sections, which has not survived. Many modern scholars also believe that Hypatia may have edited the surviving text of Ptolemy's Almagest, based on the title of her father Theon's commentary on Book III of the Almagest.

Hypatia constructed astrolabes and hydrometers, but did not invent either of these, which were both in use long before she was born. She was tolerant toward Christians and taught many Christian students, including Synesius, the future bishop of Ptolemais. Ancient sources record that Hypatia was widely beloved by pagans and Christians alike and that she established great influence with the political elite in Alexandria. Toward the end of her life, Hypatia advised Orestes, the Roman prefect of Alexandria, who was in the midst of a political feud with Cyril, the bishop of Alexandria. Rumors spread accusing her of preventing Orestes from reconciling with Cyril and, in March 415 AD, she was murdered by a mob of Christians led by a lector named Peter. (Full article...)
Image 7

8x8 Rook's graph

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

Rook's graphs are highly symmetric, having symmetries taking every vertex to every other vertex. In rook's graphs defined from square chessboards, more strongly, every two edges are symmetric, and every pair of vertices is symmetric to every other pair at the same distance in moves (making the graph distance-transitive). For rectangular chessboards whose width and height are relatively prime, the rook's graphs are circulant graphs. With one exception, the rook's graphs can be distinguished from all other graphs using only two properties: the numbers of triangles each edge belongs to, and the existence of a unique $4$ -cycle connecting each nonadjacent pair of vertices. (Full article...)
Image 8
Sunday Osarumwense Iyahen (3 October 1937 – 28 January 2018) was a Nigerian mathematician and politician, recognised for his contributions to the field of topological vector spaces and his service as a senator representing Bendel Central Senatorial District. Born in Benin City, Edo State, Nigeria, Iyahen was the eldest of at least seventeen children and embarked on an academic journey that led him to earn a first-class honours degree in mathematics from the University of Ibadan and later a Ph.D. and D.Sc. from the University of Keele.

Iyahen's academic career was marked by his tenure as a professor of mathematics at several universities in Nigeria and abroad. He served as the Head of the Department of Mathematics and Dean of the Faculty of Science at the University of Ibadan before joining the Institute of Technology, Benin (now known as the University of Benin), where he became the founding dean of the Faculty of Physical Sciences. His scholarly work includes over 100 published papers and contributions as editor-in-chief for mathematical journals. He was honoured with fellowships from the Nigerian Academy of Science and the Mathematical Association of Nigeria. As a politician, he was elected as a senator, where he contributed to national policy and development. (Full article...)
Image 9
A homomorphism from the flower snark J₅ into the cycle graph C₅.
It is also a retraction onto the subgraph on the central five vertices. Thus J₅ is in fact homomorphically equivalent to the core C₅.

In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.

Homomorphisms generalize various notions of graph colorings and allow the expression of an important class of constraint satisfaction problems, such as certain scheduling or frequency assignment problems.
The fact that homomorphisms can be composed leads to rich algebraic structures: a preorder on graphs, a distributive lattice, and a category (one for undirected graphs and one for directed graphs).
The computational complexity of finding a homomorphism between given graphs is prohibitive in general, but a lot is known about special cases that are solvable in polynomial time. Boundaries between tractable and intractable cases have been an active area of research. (Full article...)
Image 10
Vedic Mathematics is a book written by Indian Shankaracharya Bharati Krishna Tirtha and first published in 1965. It contains a list of mathematical techniques which were falsely claimed to contain advanced mathematical knowledge. The book was posthumously published under its deceptive title by editor V. S. Agrawala, who noted in the foreword that the claim of Vedic origin, made by the original author and implied by the title, was unsupported.

Neither Krishna Tirtha nor Agrawala were able to produce sources, and scholars unanimously note it to be a compendium of methods for increasing the speed of elementary mathematical calculations sharing no overlap with historical mathematical developments during the Vedic period. Nonetheless, there has been a proliferation of publications in this area and multiple attempts to integrate the subject into mainstream education at the state level by right-wing Hindu nationalist governments. (Full article...)
Image 11
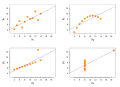
The Theil–Sen estimator of a set of sample points with outliers (black line) compared to the non-robust ordinary least squares line for the same set (blue). The dashed green line represents the ground truth from which the samples were generated.

In non-parametric statistics, the Theil–Sen estimator is a method for robustly fitting a line to sample points in the plane (simple linear regression) by choosing the median of the slopes of all lines through pairs of points. It has also been called Sen's slope estimator, slope selection, the single median method, the Kendall robust line-fit method, and the Kendall–Theil robust line. It is named after Henri Theil and Pranab K. Sen, who published papers on this method in 1950 and 1968 respectively, and after Maurice Kendall because of its relation to the Kendall tau rank correlation coefficient.

Theil-Sen regression has several advantages over Ordinary least squares regression. It is insensitive to outliers. It can be used for significance tests even when residuals are not normally distributed. It can be significantly more accurate than non-robust simple linear regression (least squares) for skewed and heteroskedastic data, and competes well against least squares even for normally distributed data in terms of statistical power. It has been called "the most popular nonparametric technique for estimating a linear trend". There are fast algorithms for efficiently computing the parameters. (Full article...)
Image 12
17 indivisible camels

The 17-animal inheritance puzzle is a mathematical puzzle involving unequal but fair allocation of indivisible goods, usually stated in terms of inheritance of a number of large animals (17 camels, 17 horses, 17 elephants, etc.) which must be divided in some stated proportion among a number of beneficiaries. It is a common example of an apportionment problem.

Despite often being framed as a puzzle, it is more an anecdote about a curious calculation than a problem with a clear mathematical solution. Beyond recreational mathematics and mathematics education, the story has been repeated as a parable with varied metaphorical meanings. (Full article...)

Did you know

... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
... that Ewa Ligocka cooked another mathematician's goose?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
... that after Archimedes first defined convex curves, mathematicians lost interest in their analysis until the 19th century, more than two millennia later?

Did you know...

... that the Life without Death cellular automaton, a mathematical model of pattern formation, is a variant of Conway's Game of Life in which cells, once brought to life, never die?
... that one can list every positive rational number without repetition by breadth-first traversal of the Calkin–Wilf tree?
... that the Hadwiger conjecture implies that the external surface of any three-dimensional convex body can be illuminated by only eight light sources, but the best proven bound is that 16 lights are sufficient?
... that an equitable coloring of a graph, in which the numbers of vertices of each color are as nearly equal as possible, may require far more colors than a graph coloring without this constraint?
... that no matter how biased a coin one uses, flipping a coin to determine whether each edge is present or absent in a countably infinite graph will always produce the same graph, the Rado graph?
...that it is possible to stack identical dominoes off the edge of a table to create an arbitrarily large overhang?
...that in Floyd's algorithm for cycle detection, the tortoise and hare move at very different speeds, but always finish at the same spot?

Featured pictures

Image 1Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 25Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 25Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

Our website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.

Portal:Mathematics

Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.