Halowentelbaan

Halowentelbaan

Poolaansig.

Ewenaaraansig.

Animasie van SOHO se wentelbaan
      Aarde ·       SOHO

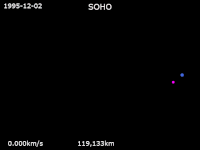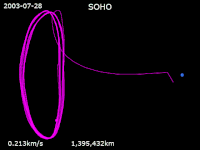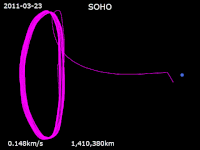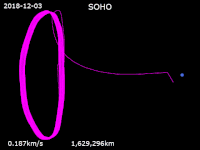
'n Halowentelbaan is 'n periodieke, driedimensionele wentelbaan naby een die Lagrange-punte L₁, L₂ of L₃ van 'n stelsel met twee wentelende liggame. Hoewel 'n Langrange-punt net 'n punt in die leë ruimte is, kan iets in 'n wentelbaan daarom beweeg. Dit is die gevolg van die swaartekragaantrekking wat die twee liggame op 'n ruimtetuig of ander liggaam het.

Halowentelbane bestaan in enige wentelende stelsel met drie liggame, waarin die satelliet die derde liggaam is: stelsels soos die Son en Aarde of die Aarde en Maan. Omdat halowentelbane onstabiel is en 'n satelliet dus uit die wentelbaan kan beweeg, moet 'n kunsmatige mag op die satelliet uitgeoefen word om dit in sy wentelbaan te hou.

Die meeste kunsmatige satelliete in halowentelbane is wetenskaplike instrumente, soos ruimteteleskope.

Wanneer ander invloede afwesig is, is wentelbane om die Lagrange-punte L₄ en L₅ dinamies stabiel, solank die verhouding van die twee hoofliggame se massa groter as 25 is.^[1] Die natuurlike dinamika hou die satelliet in die omgewing van die Lagrange-punt sonder dat 'n kunsmatige aanpassing nodig is, selfs wanneer die ewewig effens versteur word.^[2]

Die wentelbane kan egter deur ander groot voorwerpe versteur word. Wentelbane by die Aarde-Maan-stelsel se L₄- en L₅-punt kan net 'n paar miljoen jaar duur in plaas van miljarde jare weens versteurings deur die planete.^[3]

1. ↑ "A230242 - Decimal expansion of (25+3*sqrt(69))/2". OEIS. Besoek op 7 Januarie 2019.
2. ↑ Vallado, David A. (2007). Fundamentals of Astrodynamics and Applications (3de uitg.). Springer New York. ISBN 978-1-881883-14-2.
3. ↑ Lissauer, Jack J.; Chambers, John E. (2008). "Solar and planetary destabilization of the Earth–Moon triangular Lagrangian points". Icarus. 195 (1): 16–27. Bibcode:2008Icar..195...16L. doi:10.1016/j.icarus.2007.12.024.