Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Vektorruimte
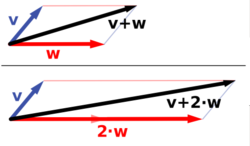
'n Vektorruimte is 'n wiskundige struktuur wat uit 'n versameling vektore bestaan, die vektore synde voorwerpe wat bymekaar gevoeg kan word (vektoraddisie) en deur skalare vermenigvuldig kan word (skalaarvermenigvuldiging). Vektorvermenigvuldigings kan op 'n vektorruimte gedefinieer word, en sommige definisies bemoontlik die meet van lengtes en hoeke in die ruimte. Die skalare betrokke by skalaarvermenigvuldiging kan reële getalle, komplekse getalle, rasionale getalle of die elemente van enige arbitrêre liggaam wees. Die bewerkings vektoraddisie en skalaarvermenigvuldiging moet aan sekere vereistes, genaamd aksiome, voldoen. 'n Voorbeeld van 'n vektorruimte is 'n Euklidiese vektorruimte, welke vektore fisiese kragte voorstel. Enige twee kragte van dieselfde tipe kan bymekaar getek word om 'n derde krag te lewer, en die vermenigvuldiging van 'n kragvektor met 'n reële skalaar lewer 'n nuwe kragvektor. In dieselfde sin, dog in 'n meer geometriese begrip, vorm vektore wat verplasing in die vlak of in driedimensionele ruimte verteenwoordig ook 'n vektorruimte.
Vektorruimtes is 'n onderwerp in lineêre algebra en word goed verstaan uit hierdie invalshoek omdat vektorruimtes gekarakteriseer word deur hul dimensies, wat rofweg die aantal onafhanklike rigtings in die ruimte is. 'n Vektorruimte kan 'n bykomende struktuur kry wanneer byvoorbeeld 'n norm of inwendige produk daarop gedefinieer word. Sulke genormde vektorruimtes of inwendige produkruimtes (soms genoem Voorhilbert-ruimtes) kom natuurlik in wiskundige analise voor, hoofsaaklik as oneindig-dimensionele funksieruimtes waar die vektore inderdaad funksies is. Analitiese probleme bepaal of vektorreekse tot enige vektor konvergeer. Dít word moontlik gemaak deur vektorruimtes met bykomende struktuur in ag te neem, hoofsaaklik ruimtes wat met 'n toepaslike topologie toegerus is, wat die inagname van naheid en kontinuïteit bewerkstellig. Hierdie topologiese vektorruimtes, veral Banach-ruimtes en Hilbert-ruimtes, bring 'n ryker teorie na vore.
Die eerste idees wat tot die konsep van vektorruimtes gelei het, het in die 17de eeu ontstaan uit analitiese meetkunde, matrikse, stelsels lineêre vergelykings, en Euklidiese vektore. Die moderne, abstrakte behandeling van vektorruimtes wat in die laat 19de eeu deur die Italiaanse wiskundige Guiseppe Peano geformaliseer is, behels veralgemenings van Euklidiese ruimte, en die meeste van die teorie kan as uitbreidings van die klassieke geometriese idees van lyne, vlakke en hul hoër-dimensionele analoë gesien word.
Vektorruimtes het toepassings wyd deur wiskunde, wetekenskap en ingenieurswese. Dit is die toepaslike lineêr-algebraïese idee om stelsels lineêre vergelykings mee te behandel, dit bied 'n raamwerk vir Fourier-uitbreiding, en dit bied 'n omgewing vir die oplos van parsiële differensiaalvergelykings. Vektorruimtes voorsien boonop 'n abstrakte, koördinaatvrye wyse waarmee geometriese en fisiese voorwerpe soos tensors behandel kan word. Dít op sy beurt laat die studie van lokale eienskappe van variëteite deur lineariserinsgtegnieke toe.
Previous Page Next Page


