Fformiwla cwadratig

Mewn algebra elfennol, y fformiwla cwadratig yw ateb yr hafaliad cwadratig. Mae ffyrdd eraill o ddatrys yr hafaliad cwadratig yn hytrach na defnyddio'r fformiwla cwadratig e.e. ffactoreiddio, cwblhau'r sgwâr, neu graffio. Yn aml, defnyddio'r fformiwla cwadratig yw'r ffordd hawddaf o wneud hyn.

Yr hafaliad arferol yw:

${\displaystyle ax^{2}+bx+c=0.}$

Yma, mae x yn cynrychioli gwerth anhybys, gyda a, b, ac c yn gysonyn, a a yn anhafal i 0. Gellir gwiro fod y fformiwla cwadrig yn bodloni'r hafaliad cwadratig trwy fewnosod y cyntaf i mewn i'r olaf. Gyda'r paramedriad uchod, y fformiwla cwadratig yw:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}$

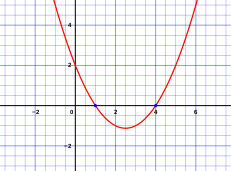
Gelwir pob un o'r atebion a roddir gan y fformiwla cwadratig yn 'wraidd' yr hafaliad cwadratig. O ran geometreg, mae'r gwreiddiau hyn yn cynrychioli'r gwerthoedd x unrhyw barabola - a roddir yn benodol fel y = ax² + bx + c - yn croesi'r echel x. Yn ogystal â bod yn fformiwla a fydd yn cynhyrchu seros unrhyw parabola, bydd y fformiwla cwadratig yn rhoi echel cymesuredd y parabola, a gellir ei ddefnyddio i benderfynu sawl sero real sydd gan yr hafaliad cwadratig.^[1][2]

1. ↑ Rich, Barnett; Schmidt, Philip (2004), Schaum's Outline of Theory and Problems of Elementary Algebra, The McGraw–Hill Companies, ISBN 0-07-141083-X, https://books.google.com/books?id=8PRU9cTKprsC, Chapter 13 §4.4, p. 291
2. ↑ Li, Xuhui. An Investigation of Secondary School Algebra Teachers' Mathematical Knowledge for Teaching Algebraic Equation Solving, p. 56 (ProQuest, 2007): "The quadratic formula is the most general method for solving quadratic equations and is derived from another general method: completing the square."