Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Urbild (Mathematik)
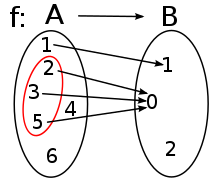
In der Mathematik ist das Urbild ein Begriff, der im Zusammenhang mit Funktionen verwendet wird. Für eine Funktion ist das Urbild einer Menge jene Teilmenge der Definitionsmenge , deren Elemente auf die vorher festgelegte Untermenge der Zielmenge abgebildet werden. Das Urbild ist also die Antwort auf die Frage: Welche Elemente aus der Definitionsmenge werden auf Elemente der Menge abgebildet? Man sagt dann auch Urbild von unter .
Das Urbild eines einzelnen Elements der Zielmenge ist die aus allen mit bestehende Teilmenge der Definitionsmenge. Das Urbild der Bildmenge (und natürlich erst recht der ganzen Zielmenge ) ist genau die Definitionsmenge , da Funktionen linkstotal sind, also jedem Element der Definitionsmenge mindestens ein Element der Zielmenge (und genau ein Element der Bildmenge) zuordnen.
Previous Page Next Page















