Bernoulli distribution

Bernoulli distribution

Probability mass function 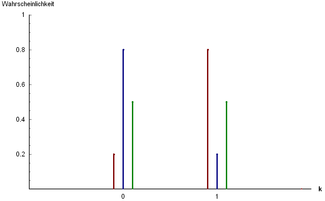Three examples of Bernoulli distribution:   ${\displaystyle P(x=0)=0{.}2}$ and ${\displaystyle P(x=1)=0{.}8}$   ${\displaystyle P(x=0)=0{.}8}$ and ${\displaystyle P(x=1)=0{.}2}$   ${\displaystyle P(x=0)=0{.}5}$ and ${\displaystyle P(x=1)=0{.}5}$
Parameters	${\displaystyle 0\leq p\leq 1}$ ${\displaystyle q=1-p}$
Support	${\displaystyle k\in \{0,1\}}$
PMF	${\displaystyle {\begin{cases}q=1-p&{\text{if }}k=0\\p&{\text{if }}k=1\end{cases}}}$
CDF	${\displaystyle {\begin{cases}0&{\text{if }}k<0\\1-p&{\text{if }}0\leq k<1\\1&{\text{if }}k\geq 1\end{cases}}}$
Mean	${\displaystyle p}$
Median	${\displaystyle {\begin{cases}0&{\text{if }}p<1/2\\\left[0,1\right]&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}}$
Mode	${\displaystyle {\begin{cases}0&{\text{if }}p<1/2\\0,1&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}}$
Variance	${\displaystyle p(1-p)=pq}$
MAD	${\displaystyle 2p(1-p)=2pq}$
Skewness	${\displaystyle {\frac {q-p}{\sqrt {pq}}}}$
Excess kurtosis	${\displaystyle {\frac {1-6pq}{pq}}}$
Entropy	${\displaystyle -q\ln q-p\ln p}$
MGF	${\displaystyle q+pe^{t}}$
CF	${\displaystyle q+pe^{it}}$
PGF	${\displaystyle q+pz}$
Fisher information	${\displaystyle {\frac {1}{pq}}}$

Part of a series on statistics
Probability theory
Probability Axioms Determinism System Indeterminism Randomness
Probability space Sample space Event Collectively exhaustive events Elementary event Mutual exclusivity Outcome Singleton Experiment Bernoulli trial Probability distribution Bernoulli distribution Binomial distribution Exponential distribution Normal distribution Pareto distribution Poisson distribution Probability measure Random variable Bernoulli process Continuous or discrete Expected value Variance Markov chain Observed value Random walk Stochastic process
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram
v t e

In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,^[1] is the discrete probability distribution of a random variable which takes the value 1 with probability ${\displaystyle p}$ and the value 0 with probability ${\displaystyle q=1-p}$. Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcomes that are Boolean-valued: a single bit whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails", respectively, and p would be the probability of the coin landing on heads (or vice versa where 1 would represent tails and p would be the probability of tails). In particular, unfair coins would have ${\displaystyle p\neq 1/2.}$

The Bernoulli distribution is a special case of the binomial distribution where a single trial is conducted (so n would be 1 for such a binomial distribution). It is also a special case of the two-point distribution, for which the possible outcomes need not be 0 and 1. ^[2]