Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Correlation function
This article needs additional citations for verification. (December 2023) |
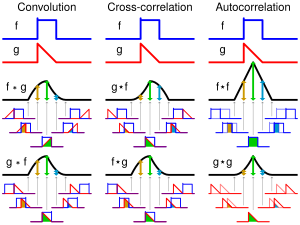
A correlation function is a function that gives the statistical correlation between random variables, contingent on the spatial or temporal distance between those variables.[1] If one considers the correlation function between random variables representing the same quantity measured at two different points, then this is often referred to as an autocorrelation function, which is made up of autocorrelations. Correlation functions of different random variables are sometimes called cross-correlation functions to emphasize that different variables are being considered and because they are made up of cross-correlations.
Correlation functions are a useful indicator of dependencies as a function of distance in time or space, and they can be used to assess the distance required between sample points for the values to be effectively uncorrelated. In addition, they can form the basis of rules for interpolating values at points for which there are no observations.
Correlation functions used in astronomy, financial analysis, econometrics, and statistical mechanics differ only in the particular stochastic processes they are applied to. In quantum field theory there are correlation functions over quantum distributions.
- ^ Pal, Manoranjan; Bharati, Premananda (2019). "Introduction to Correlation and Linear Regression Analysis". Applications of Regression Techniques. Springer, Singapore. pp. 1–18. doi:10.1007/978-981-13-9314-3_1. Retrieved December 14, 2023.
Previous Page Next Page


