Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.

Responsive image

Elementary cellular automaton

An animation of how an evolution is determined in Rule 30, one of the 256 possible rules of elementary cellular automata.
All the 256 elementary cellular automaton rules[1] (click or tap to enlarge).

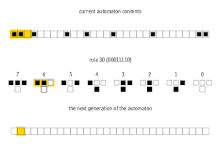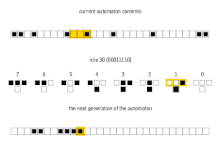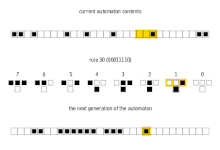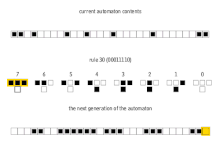
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states (labeled 0 and 1) and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors. There is an elementary cellular automaton (rule 110, defined below) which is capable of universal computation, and as such it is one of the simplest possible models of computation.

  1. ^ R.Ugalde, Laurence. "Elementary cellular automaton in the Fōrmulæ programming language". Fōrmulæ. Retrieved June 9, 2024.

Previous Page Next Page






Autómata celular elemental Spanish اتوماتای سلولی ساده FA Elementaire cellulaire automaat Dutch Элементарный клеточный автомат Russian Елементарні клітинні автомати Ukrainian

Responsive image

Responsive image