Elongated square gyrobicupola

Elongated square gyrobicupola
Elongated square gyrobicupola
Type	Canonical,; Johnson; J36 – J37 – J38
Faces	8 triangles; 18 squares
Edges	48
Vertices	24
Vertex configuration
Symmetry group
Properties	convex,; singular vertex figure
Net

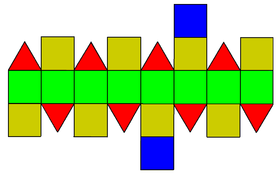In geometry, the elongated square gyrobicupola is a polyhedron constructed by two square cupolas attaching onto the bases of octagonal prism, with one of them rotated. It was once mistakenly considered a rhombicuboctahedron by many mathematicians. It is not considered to be an Archimedean solid because it lacks a set of global symmetries that map every vertex to every other vertex, unlike the 13 Archimedean solids. It is also a canonical polyhedron. For this reason, it is also known as pseudo-rhombicuboctahedron, Miller solid,^[1] or Miller–Askinuze solid.^[2]

^ Cite error: The named reference cromwell was invoked but never defined (see the help page).
^ Cite error: The named reference johnson was invoked but never defined (see the help page).

[cromwell-1] Cite error: The named reference cromwell was invoked but never defined (see the help page).

[johnson-2] Cite error: The named reference johnson was invoked but never defined (see the help page).

[1]

[2]

Elongated square gyrobicupola

Type	Canonical, Johnson $J 36 - J 37 - J 38$
Faces	8 triangles 18 squares
Edges	48
Vertices	24
Vertex configuration	$8+16(3\cdot 4^{3})$
Symmetry group	$D_{4\mathrm {d} }$
Properties	convex, singular vertex figure
Net

Our website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.

Elongated square gyrobicupola

Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.