Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
F-test
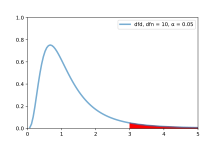
An F-test is a statistical test that compares variances. It's used to determine if the variances of two samples, or if the ratios of variances among multiple samples, are significantly different. The test calculates a statistic, represented by the random variable F, and checks if it follows an F-distribution. This check is valid if the null hypothesis is true and standard assumptions about the errors (ε) in the data hold.[1]
F-tests are frequently used to compare different statistical models and find the one that best describes the population the data came from. When models are created using the least squares method, the resulting F-tests are often called "exact" F-tests. The F-statistic was developed by Ronald Fisher in the 1920s as the variance ratio and was later named in his honor by George W. Snedecor.[2]
- ^ Berger, Paul D.; Maurer, Robert E.; Celli, Giovana B. (2018). Experimental Design. Cham: Springer International Publishing. p. 108. doi:10.1007/978-3-319-64583-4. ISBN 978-3-319-64582-7.
- ^ Lomax, Richard G. (2007). Statistical Concepts: A Second Course. Lawrence Erlbaum Associates. p. 10. ISBN 978-0-8058-5850-1.
Previous Page Next Page


