Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Fermat's right triangle theorem
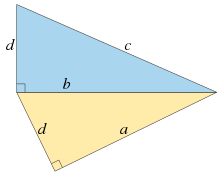
Fermat's right triangle theorem is a non-existence proof in number theory, published in 1670 among the works of Pierre de Fermat, soon after his death. It is the only complete proof given by Fermat.[1] It has many equivalent formulations, one of which was stated (but not proved) in 1225 by Fibonacci. In its geometric forms, it states:
- A right triangle in the Euclidean plane for which all three side lengths are rational numbers cannot have an area that is the square of a rational number. The area of a rational-sided right triangle is called a congruent number, so no congruent number can be square.
- A right triangle and a square with equal areas cannot have all sides commensurate with each other.
- There do not exist two integer-sided right triangles in which the two legs of one triangle are the leg and hypotenuse of the other triangle.
More abstractly, as a result about Diophantine equations (integer or rational-number solutions to polynomial equations), it is equivalent to the statements that:
- If three square numbers form an arithmetic progression, then the gap between consecutive numbers in the progression (called a congruum) cannot itself be square.
- The only rational points on the elliptic curve are the three trivial points with and .
- The quartic equation has no nonzero integer solution.
An immediate consequence of the last of these formulations is that Fermat's Last Theorem is true in the special case that its exponent is 4.
- ^ Edwards (2000). Many subsequent mathematicians published proofs, including Gottfried Wilhelm Leibniz (1678), Leonhard Euler (1747), and Bernard Frenicle de Bessy (before 1765); see Dickson (1920) and Goldstein (1995).
Previous Page Next Page














