Goldberg polyhedron

Icosahedral Goldberg polyhedra, with pentagons in red

GP(1,4) = {5+,3}1,4	GP(4,4) = {5+,3}4,4
GP(7,0) = {5+,3}7,0	GP(3,5) = {5+,3}3,5
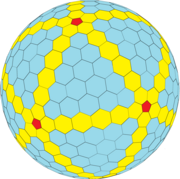
GP(10,0) = {5+,3}10,0, equilateral and spherical

In mathematics, and more specifically in polyhedral combinatorics, a Goldberg polyhedron is a convex polyhedron made from hexagons and pentagons. They were first described in 1937 by Michael Goldberg (1902–1990). They are defined by three properties: each face is either a pentagon or hexagon, exactly three faces meet at each vertex, and they have rotational icosahedral symmetry. They are not necessarily mirror-symmetric; e.g. GP(5,3) and GP(3,5) are enantiomorphs of each other. A Goldberg polyhedron is a dual polyhedron of a geodesic polyhedron.

A consequence of Euler's polyhedron formula is that a Goldberg polyhedron always has exactly 12 pentagonal faces. Icosahedral symmetry ensures that the pentagons are always regular and that there are always 12 of them. If the vertices are not constrained to a sphere, the polyhedron can be constructed with planar equilateral (but not in general equiangular) faces.

Simple examples of Goldberg polyhedra include the dodecahedron and truncated icosahedron. Other forms can be described by taking a chess knight move from one pentagon to the next: first take m steps in one direction, then turn 60° to the left and take n steps. Such a polyhedron is denoted GP(m,n). A dodecahedron is GP(1,0), and a truncated icosahedron is GP(1,1).

A similar technique can be applied to construct polyhedra with tetrahedral symmetry and octahedral symmetry. These polyhedra will have triangles or squares rather than pentagons. These variations are given Roman numeral subscripts denoting the number of sides on the non-hexagon faces: GP_III(n,m), GP_IV(n,m), and GP_V(n,m).