Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Graded poset
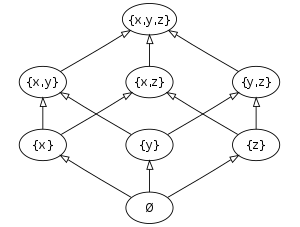
In mathematics, in the branch of combinatorics, a graded poset is a partially-ordered set (poset) P equipped with a rank function ρ from P to the set N of all natural numbers. ρ must satisfy the following two properties:
- The rank function is compatible with the ordering, meaning that for all x and y in the order, if x < y then ρ(x) < ρ(y), and
- The rank is consistent with the covering relation of the ordering, meaning that for all x and y, if y covers x then ρ(y) = ρ(x) + 1.
The value of the rank function for an element of the poset is called its rank. Sometimes a graded poset is called a ranked poset but that phrase has other meanings; see Ranked poset. A rank or rank level of a graded poset is the subset of all the elements of the poset that have a given rank value.[1][2]
Graded posets play an important role in combinatorics and can be visualized by means of a Hasse diagram.
- ^ Stanley, Richard (1984), "Quotients of Peck posets", Order, 1 (1): 29–34, doi:10.1007/BF00396271, MR 0745587, S2CID 14857863.
- ^ Butler, Lynne M. (1994), Subgroup Lattices and Symmetric Functions, Memoirs of the American Mathematical Society, vol. 539, American Mathematical Society, p. 151, ISBN 9780821826003.
Previous Page Next Page


