Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Monomorphism
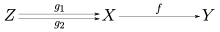
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation .
In the more general setting of category theory, a monomorphism (also called a monic morphism or a mono) is a left-cancellative morphism. That is, an arrow f : X → Y such that for all objects Z and all morphisms g1, g2: Z → X,
Monomorphisms are a categorical generalization of injective functions (also called "one-to-one functions"); in some categories the notions coincide, but monomorphisms are more general, as in the examples below.
In the setting of posets intersections are idempotent: the intersection of anything with itself is itself. Monomorphisms generalize this property to arbitrary categories. A morphism is a monomorphism if it is idempotent with respect to pullbacks.
The categorical dual of a monomorphism is an epimorphism, that is, a monomorphism in a category C is an epimorphism in the dual category Cop. Every section is a monomorphism, and every retraction is an epimorphism.
Previous Page Next Page





