Multigraph

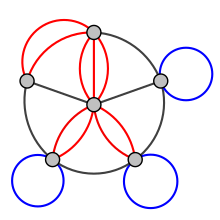
In mathematics, and more specifically in graph theory, a multigraph is a graph which is permitted to have multiple edges (also called parallel edges^[1]), that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge.

There are 2 distinct notions of multiple edges:

• Edges without own identity: The identity of an edge is defined solely by the two nodes it connects. In this case, the term "multiple edges" means that the same edge can occur several times between these two nodes.
• Edges with own identity: Edges are primitive entities just like nodes. When multiple edges connect two nodes, these are different edges.

A multigraph is different from a hypergraph, which is a graph in which an edge can connect any number of nodes, not just two.

For some authors, the terms pseudograph and multigraph are synonymous. For others, a pseudograph is a multigraph that is permitted to have loops.