Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Phase velocity

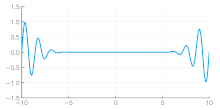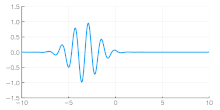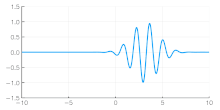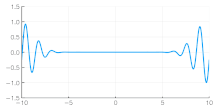

The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as
Equivalently, in terms of the wave's angular frequency ω, which specifies angular change per unit of time, and wavenumber (or angular wave number) k, which represent the angular change per unit of space,
To gain some basic intuition for this equation, we consider a propagating (cosine) wave A cos(kx − ωt). We want to see how fast a particular phase of the wave travels. For example, we can choose kx - ωt = 0, the phase of the first crest. This implies kx = ωt, and so v = x / t = ω / k.
Formally, we let the phase φ = kx - ωt and see immediately that ω = -dφ / dt and k = dφ / dx. So, it immediately follows that
As a result, we observe an inverse relation between the angular frequency and wavevector. If the wave has higher frequency oscillations, the wavelength must be shortened for the phase velocity to remain constant.[2] Additionally, the phase velocity of electromagnetic radiation may – under certain circumstances (for example anomalous dispersion) – exceed the speed of light in vacuum, but this does not indicate any superluminal information or energy transfer.[citation needed] It was theoretically described by physicists such as Arnold Sommerfeld and Léon Brillouin.
The previous definition of phase velocity has been demonstrated for an isolated wave. However, such a definition can be extended to a beat of waves, or to a signal composed of multiple waves. For this it is necessary to mathematically write the beat or signal as a low frequency envelope multiplying a carrier. Thus the phase velocity of the carrier determines the phase velocity of the wave set.[3]
- ^ Nemirovsky, Jonathan; Rechtsman, Mikael C; Segev, Mordechai (9 April 2012). "Negative radiation pressure and negative effective refractive index via dielectric birefringence". Optics Express. 20 (8): 8907–8914. Bibcode:2012OExpr..20.8907N. doi:10.1364/OE.20.008907. PMID 22513601.
- ^ "Phase, Group, and Signal Velocity". Mathpages.com. Retrieved 2011-07-24.
- ^ "Phase Velocity: Waves and Signals". electroagenda.com.
Previous Page Next Page





