Pushforward (differential)

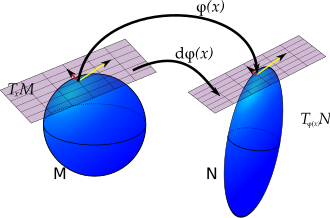
In differential geometry, pushforward is a linear approximation of smooth maps (formulating manifold) on tangent spaces. Suppose that ${\displaystyle \varphi \colon M\to N}$ is a smooth map between smooth manifolds; then the differential of ${\displaystyle \varphi }$ at a point ${\displaystyle x}$, denoted ${\displaystyle \mathrm {d} \varphi _{x}}$, is, in some sense, the best linear approximation of ${\displaystyle \varphi }$ near ${\displaystyle x}$. It can be viewed as a generalization of the total derivative of ordinary calculus. Explicitly, the differential is a linear map from the tangent space of ${\displaystyle M}$ at ${\displaystyle x}$ to the tangent space of ${\displaystyle N}$ at ${\displaystyle \varphi (x)}$, ${\displaystyle \mathrm {d} \varphi _{x}\colon T_{x}M\to T_{\varphi (x)}N}$. Hence it can be used to push tangent vectors on ${\displaystyle M}$ forward to tangent vectors on ${\displaystyle N}$. The differential of a map ${\displaystyle \varphi }$ is also called, by various authors, the derivative or total derivative of ${\displaystyle \varphi }$.