Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Pythagorean interval
The article's lead section may need to be rewritten. (November 2010) |
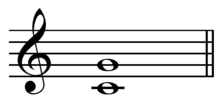
In musical tuning theory, a Pythagorean interval is a musical interval with a frequency ratio equal to a power of two divided by a power of three, or vice versa.[1] For instance, the perfect fifth with ratio 3/2 (equivalent to 31/ 21) and the perfect fourth with ratio 4/3 (equivalent to 22/ 31) are Pythagorean intervals.
All the intervals between the notes of a scale are Pythagorean if they are tuned using the Pythagorean tuning system. However, some Pythagorean intervals are also used in other tuning systems. For instance, the above-mentioned Pythagorean perfect fifth and fourth are also used in just intonation.
- ^ Benson, Donald C. (2003). A Smoother Pebble: Mathematical Explorations, p.56. ISBN 978-0-19-514436-9. "The frequency ratio of every Pythagorean interval is a ratio between a power of two and a power of three...confirming the Pythagorean requirements that all intervals be associated with ratios of whole numbers."
Previous Page Next Page


