Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Restricted Boltzmann machine
| Part of a series on |
| Machine learning and data mining |
|---|
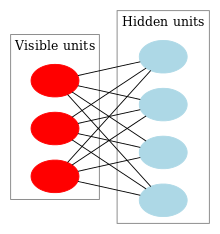
A restricted Boltzmann machine (RBM) (also called a restricted Sherrington–Kirkpatrick model with external field or restricted stochastic Ising–Lenz–Little model) is a generative stochastic artificial neural network that can learn a probability distribution over its set of inputs.[1]
RBMs were initially proposed under the name Harmonium by Paul Smolensky in 1986,[2] and rose to prominence after Geoffrey Hinton and collaborators used fast learning algorithms for them in the mid-2000s. RBMs have found applications in dimensionality reduction,[3] classification,[4] collaborative filtering,[5] feature learning,[6] topic modelling,[7] immunology,[8] and even many‑body quantum mechanics.[9] [10] [11]
They can be trained in either supervised or unsupervised ways, depending on the task.[citation needed]
As their name implies, RBMs are a variant of Boltzmann machines, with the restriction that their neurons must form a bipartite graph:
- a pair of nodes from each of the two groups of units (commonly referred to as the "visible" and "hidden" units respectively) may have a symmetric connection between them; and
- there are no connections between nodes within a group.
By contrast, "unrestricted" Boltzmann machines may have connections between hidden units. This restriction allows for more efficient training algorithms than are available for the general class of Boltzmann machines, in particular the gradient-based contrastive divergence algorithm.[12]
Restricted Boltzmann machines can also be used in deep learning networks. In particular, deep belief networks can be formed by "stacking" RBMs and optionally fine-tuning the resulting deep network with gradient descent and backpropagation.[13]
- ^ Sherrington, David; Kirkpatrick, Scott (1975), "Solvable Model of a Spin-Glass", Physical Review Letters, 35 (35): 1792–1796, Bibcode:1975PhRvL..35.1792S, doi:10.1103/PhysRevLett.35.1792
- ^ Smolensky, Paul (1986). "Chapter 6: Information Processing in Dynamical Systems: Foundations of Harmony Theory" (PDF). In Rumelhart, David E.; McLelland, James L. (eds.). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations. MIT Press. pp. 194–281. ISBN 0-262-68053-X.
- ^ Hinton, G. E.; Salakhutdinov, R. R. (2006). "Reducing the Dimensionality of Data with Neural Networks" (PDF). Science. 313 (5786): 504–507. Bibcode:2006Sci...313..504H. doi:10.1126/science.1127647. PMID 16873662. S2CID 1658773. Archived from the original (PDF) on 2015-12-23. Retrieved 2015-12-02.
- ^ Larochelle, H.; Bengio, Y. (2008). Classification using discriminative restricted Boltzmann machines (PDF). Proceedings of the 25th international conference on Machine learning - ICML '08. p. 536. doi:10.1145/1390156.1390224. ISBN 978-1-60558-205-4.
- ^ Salakhutdinov, R.; Mnih, A.; Hinton, G. (2007). Restricted Boltzmann machines for collaborative filtering. Proceedings of the 24th international conference on Machine learning - ICML '07. p. 791. doi:10.1145/1273496.1273596. ISBN 978-1-59593-793-3.
- ^ Coates, Adam; Lee, Honglak; Ng, Andrew Y. (2011). An analysis of single-layer networks in unsupervised feature learning (PDF). International Conference on Artificial Intelligence and Statistics (AISTATS). Archived from the original (PDF) on 2014-12-20. Retrieved 2014-12-19.
- ^ Ruslan Salakhutdinov and Geoffrey Hinton (2010). Replicated softmax: an undirected topic model Archived 2012-05-25 at the Wayback Machine. Neural Information Processing Systems 23.
- ^ Bravi, Barbara; Di Gioacchino, Andrea; Fernandez-de-Cossio-Diaz, Jorge; Walczak, Aleksandra M; Mora, Thierry; Cocco, Simona; Monasson, Rémi (2023-09-08). Bitbol, Anne-Florence; Eisen, Michael B (eds.). "A transfer-learning approach to predict antigen immunogenicity and T-cell receptor specificity". eLife. 12: e85126. doi:10.7554/eLife.85126. ISSN 2050-084X. PMC 10522340. PMID 37681658.
- ^ Carleo, Giuseppe; Troyer, Matthias (2017-02-10). "Solving the quantum many-body problem with artificial neural networks". Science. 355 (6325): 602–606. arXiv:1606.02318. Bibcode:2017Sci...355..602C. doi:10.1126/science.aag2302. ISSN 0036-8075. PMID 28183973. S2CID 206651104.
- ^ Melko, Roger G.; Carleo, Giuseppe; Carrasquilla, Juan; Cirac, J. Ignacio (September 2019). "Restricted Boltzmann machines in quantum physics". Nature Physics. 15 (9): 887–892. Bibcode:2019NatPh..15..887M. doi:10.1038/s41567-019-0545-1. ISSN 1745-2481. S2CID 256704838.
- ^ Pan, Ruizhi; Clark, Charles W. (2024). "Efficiency of neural-network state representations of one-dimensional quantum spin systems". Physical Review Research. 6: 023193. arXiv:2302.00173. doi:10.1103/PhysRevResearch.6.023193.
- ^ Miguel Á. Carreira-Perpiñán and Geoffrey Hinton (2005). On contrastive divergence learning. Artificial Intelligence and Statistics.
- ^ Hinton, G. (2009). "Deep belief networks". Scholarpedia. 4 (5): 5947. Bibcode:2009SchpJ...4.5947H. doi:10.4249/scholarpedia.5947.
Previous Page Next Page
Màquina de Boltzmann restrictiva Catalan Máquina de Boltzmann restringida Spanish ماشین بولتزمن محدود شده FA Machine de Boltzmann restreinte French Macchina di Boltzmann ristretta Italian 제한된 볼츠만 머신 Korean Ограниченная машина Больцмана Russian Обмежена машина Больцмана Ukrainian Máy Boltzmann hạn chế VI 受限玻尔兹曼机 Chinese


