Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Right ascension
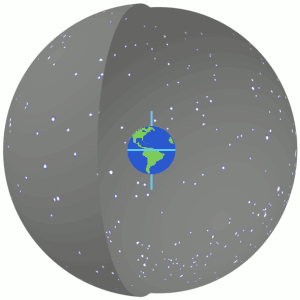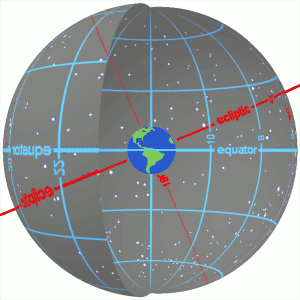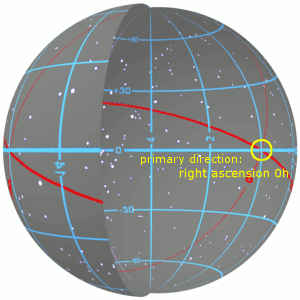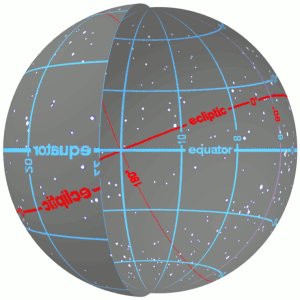
Right ascension (abbreviated RA; symbol α) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the (hour circle of the) point in question above the Earth.[1] When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system.
An old term, right ascension (Latin: ascensio recta)[2] refers to the ascension, or the point on the celestial equator that rises with any celestial object as seen from Earth's equator, where the celestial equator intersects the horizon at a right angle. It contrasts with oblique ascension, the point on the celestial equator that rises with any celestial object as seen from most latitudes on Earth, where the celestial equator intersects the horizon at an oblique angle.[3]
- ^ U.S. Naval Observatory Nautical Almanac Office (1992). Seidelmann, P. Kenneth (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. p. 735. ISBN 0-935702-68-7.
- ^ Blaeu, Guilielmi (1668). Institutio Astronomica. Apud Johannem Blaeu. p. 65., "Ascensio recta Solis, stellæ, aut alterius cujusdam signi, est gradus æquatorus cum quo simul exoritur in sphæra recta"; roughly translated, "Right ascension of the Sun, stars, or any other sign, is the degree of the equator that rises together in a right sphere"
- ^ Lathrop, John (1821). A Compendious Treatise on the Use of Globes and Maps. Wells and Lilly and J.W. Burditt, Boston. pp. 29, 39.
Previous Page Next Page


