Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Runge's phenomenon
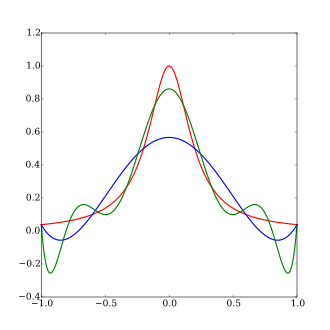
The function
A fifth order polynomial interpolation (exact replication of the red curve at 6 points)
A ninth order polynomial interpolation (exact replication of the red curve at 10 points)
In the mathematical field of numerical analysis, Runge's phenomenon (German: [ˈʁʊŋə]) is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree over a set of equispaced interpolation points. It was discovered by Carl David Tolmé Runge (1901) when exploring the behavior of errors when using polynomial interpolation to approximate certain functions.[1] The discovery shows that going to higher degrees does not always improve accuracy. The phenomenon is similar to the Gibbs phenomenon in Fourier series approximations.
- ^ Runge, Carl (1901), "Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten", Zeitschrift für Mathematik und Physik, 46: 224–243. available at www.archive.org
Previous Page Next Page



