Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Series expansion
This article needs additional citations for verification. (August 2021) |
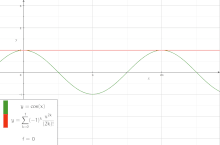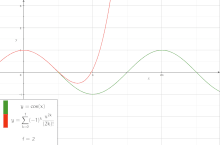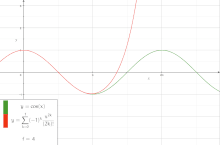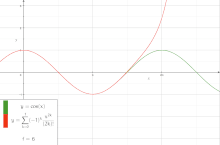
In mathematics, a series expansion is a technique that expresses a function as an infinite sum, or series, of simpler functions. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division).[1]
The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions.[2][verification needed]
- ^ "Series and Expansions". Mathematics LibreTexts. 2013-11-07. Retrieved 2021-12-24.
- ^ Gil, Amparo; Segura, Javier; Temme, Nico M. (2007-01-01). Numerical Methods for Special Functions. SIAM. ISBN 978-0-89871-782-2.
Previous Page Next Page


