Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Translational symmetry
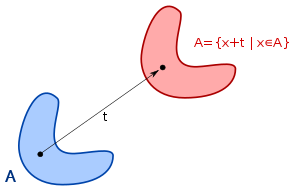
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation.
Analogously, an operator A on functions is said to be translationally invariant with respect to a translation operator if the result after applying A doesn't change if the argument function is translated. More precisely it must hold that
Laws of physics are translationally invariant under a spatial translation if they do not distinguish different points in space. According to Noether's theorem, space translational symmetry of a physical system is equivalent to the momentum conservation law.
Translational symmetry of an object means that a particular translation does not change the object. For a given object, the translations for which this applies form a group, the symmetry group of the object, or, if the object has more kinds of symmetry, a subgroup of the symmetry group.
Previous Page Next Page
تناظر انتقالي Arabic Simetria de translació Catalan Translationsinvariante Funktion German Translacia simetrio EO Simetría traslacional Spanish Symétrie de translation French Translatiesymmetrie Dutch Invariante por translação Portuguese Simetrie de translație Romanian Трансляционная симметрия Russian






