Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Kvaredro
| Kvaredro | |
| Plia nomo | Triangula piramido |

| |
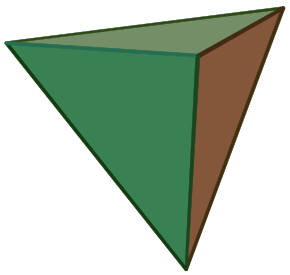
| |
| Klaku por rigardi turnantan bildon | |
| Speco | Trianguledra pluredro 3-simplaĵo |
| Vertica figuro | 3.3.3 |
| Bildo de vertico | 
|
| Bildo de reto | 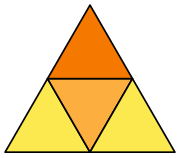
|
| Simbolo de Wythoff | 3 | 2 3 |
| Simbolo de Schläfli | {3,3} |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U01 C15 W1 |
| Simbolo de Bowers | Tet |
| Verticoj | 4 |
| Lateroj | 6 |
| Edroj | 4 |
| Edroj detale | 4{3} |
| χ | 2 |
| Geometria simetria grupo | Td |
| Duedra angulo | arccos(1/3) ~= 70,528779° |
| Duala | Mem-duala |
| Bildo de duala | 
|
Kvaredro estas pluredro komponita el 4 triangulaj edroj. Tri edroj kuniĝas je ĉiu vertico. Regula kvaredro estas kvaredro ĉe kiu la trianguloj estas regulaj. Regula kvaredro estas regula pluredro, unu el la platonaj solidoj.
Ekzistas nur unu speco de nedegenera kvaredro, kiu estas triangula piramido, alivorte ĉi ĉiuj kvaredroj estas topologie la samaj. Tamen degenera kvaredro povas esti topologie malsama, ekzemple ĝi povas esti subspeco de duvertica pluredro kun 4 edroj.
Previous Page Next Page



