Espiral sinusoidal

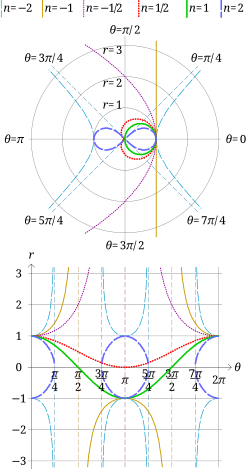
En geometría, las espirales sinusoidales son una familia de curvas definidas por la ecuación en coordenadas polares

${\displaystyle r^{n}=a^{n}\cos(n\theta )\,}$

donde a es una constante distinta de cero y n es un número racional distinto de cero. Con una rotación sobre el origen, la ecuación también se puede escribir como

${\displaystyle r^{n}=a^{n}\sin(n\theta ).\,}$

El término "espiral" es un nombre inapropiado, porque en realidad no son espirales, y a menudo tienen forma lobulada. Muchas curvas bien conocidas son espirales sinusoidales, entre las que se incluyen:

• Hipérbola equilátera (n = −2)
• Recta (n = −1)
• Parábola (n = −1/2)
• Cúbica de Tschirnhausen (n = −1/3)
• Sexteto de Cayley (n = 1/3)
• Cardioide (n = 1/2)
• Circunferencia (n = 1)
• Lemniscata de Bernoulli (n = 2)

Las curvas fueron estudiadas por primera vez por Colin Maclaurin.