Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Primera conjetura de Hardy-Littlewood
| Primera conjetura de Hardy–Littlewood | ||
|---|---|---|
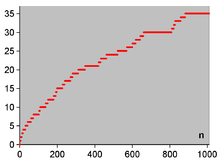 Gráfica que muestra la cantidad de números primos gemelos menores que un n dado. La primera conjetura de Hardy–Littlewood predice que hay una infinidad de ellos. | ||
| Campo | Teoría de números | |
| Conjeturado por |
G. H. Hardy John Edensor Littlewood | |
| Conjeturado en | 1923 | |
| Problema abierto | Sí | |
En teoría de números, la primera conjetura de Hardy–Littlewood[1] muestra una fórmula asintótica para estimar el número de k-tuplas de primos menores que una magnitud dada mediante la generalización del teorema de los números primos. Fue propuesta por primera vez por G. H. Hardy y John Edensor Littlewood en 1923.[2]
- ↑ Aletheia-Zomlefer, Fukshansky y Garcia, 2020.
- ↑ Hardy, G. H.; Littlewood, J. E. (1923). «Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes.». Acta Math. 44 (44): 1-70. doi:10.1007/BF02403921..
Previous Page Next Page


