Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
E (nombre)
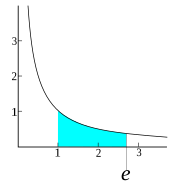
Le nombre e est la base des logarithmes naturels, c'est-à-dire le nombre défini par ln(e) = 1. Cette constante mathématique[a], également appelée nombre d'Euler[b] ou constante de Néper en référence aux mathématiciens Leonhard Euler et John Napier[c], vaut environ 2,71828.
Ce nombre est défini à la fin du XVIIe siècle, dans une correspondance entre Leibniz et Christian Huygens, comme étant la base du logarithme naturel. Autrement dit, il est caractérisé par la relation ln(e) = 1 ou de façon équivalente il est l'image de 1 par la fonction exponentielle, d'où la notation exp(x) = ex. La décomposition de cette fonction en série entière mène à la définition de e par Euler comme somme de la série[1] : Ce nombre apparaît aussi comme limite de la suite numérique de terme général et dans de nombreuses formules en analyse telles que l'identité d'Euler eiπ = −1 ou la formule de Stirling qui donne un équivalent de la factorielle. Il intervient aussi en théorie des probabilités ou en combinatoire.
Euler démontre en 1737 que e est irrationnel, donc que son développement décimal n'est pas périodique, et en donne une première approximation avec 23 décimales. Il explicite pour cela son développement en fraction continue. En 1873, Charles Hermite montre que le nombre e est même transcendant, c'est-à-dire qu'il n'est racine d'aucun polynôme non nul à coefficients entiers.
Erreur de référence : Des balises <ref> existent pour un groupe nommé « alpha », mais aucune balise <references group="alpha"/> correspondante n’a été trouvée
- ↑ (en) Encyclopedic Dictionary of Mathematics, 142.D.
Previous Page Next Page




