Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Fermi-Diracova statistika
U kvantnoj statističkoj fizici, Fermi-Diracova statistika opisuje distribuciju fermiona po energetskim stanjima, u stanju termodinamičke ravnoteže. Za razliku od klasične fizike i klasične statističke fizike, u ovom slučaju čestice se ponašaju tako da:
a) nije moguće razlučiti dva fermiona, to su indentične čestice
b) vrijedi Paulijev princip isključenja, prema kojemu se dva fermiona ne mogu istovremeno nalaziti u istom kvantnom stanju.
Za Fermi-Diracovu statistiku, očekivani broj čestica koje se nalaze u stanju s energijom dan je kao:
gdje je:
- broj čestica u stanju i
- energija stanja i
- je degeneracija stanja i (broj stanja s energijom ),
- kemijski potencijal, često nazvan Fermijeva energija
- Boltzmannova konstanta
- apsolutna temperatura
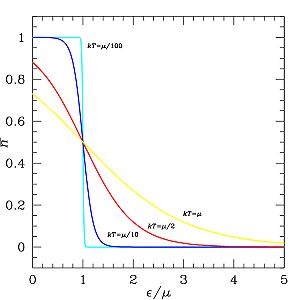
U slučaju kada je Fermijeva energija i nema degeneracije, tj. , funkcija se naziva Fermijeva funkcija:
Mnoštvo fermiona koji međusobno ne intereagiraju i slijede Fermi-Diracovu statistiku naziva se Fermionski plin.
Ova statistička distribucija uvedena je 1926.g. od strane Enrica Fermija i Paula A. M. Diraca. Vjerojatno najpoznatiji primjer primjene ove distribucije je opis vodljivih elektrona u metalu, koji je dao Arnold Sommerfeld 1927.g.
Previous Page Next Page
إحصاء فيرمي وديراك Arabic Fermi–Dirak statistikası AZ Статыстыка Фермі — Дзірака BE Статистика на Ферми-Дирак Bulgarian ফের্মি–ডির্যাক পরিসংখ্যান Bengali/Bangla Fermi–Diracova statistika BS Estadística de Fermi-Dirac Catalan Fermiho–Diracovo rozdělení Czech Fermi-Dirac-Statistik German Fermi–Dirac statistics English














