Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Epigrafico (matematica)
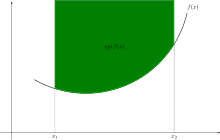
In analisi matematica, l'epigrafico di una funzione
definita su un insieme è l'insieme di punti che stanno al di sopra o sul grafico della funzione:
Se è un sottoinsieme di , l'epigrafico è un sottoinsieme di .
Previous Page Next Page







