Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.

Responsive image

Problema di Apollonio

Abbozzo geometria
Questa voce sull'argomento geometria è solo un abbozzo.
Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento.
Date 3 circonferenze distinte si vogliono costruire 8 circonferenze tangenti ad esse. Si determinano innanzitutto i luoghi geometrici dei centri di tutte le circonferenze, tangenti a ogni coppia delle circonferenze date. Ogni coppia delle circonferenze date ammette due iperboli con la proprietà del detto luogo geometrico. Poiché vi sono tre circonferenze date, il numero totale delle iperboli è 6. I punti comuni a ogni 3 rami di tali iperboli sono i centri delle 8 circonferenze cercate

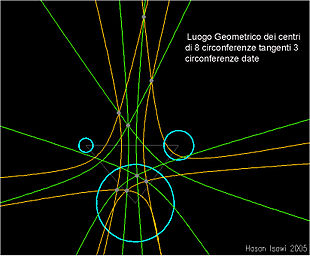
Il problema di Apollonio (dal nome dello scienziato Apollonio di Perga) è un problema geometrico di tangenza tra circonferenze ed è formulato nei seguenti termini:

«Date tre circonferenze, eventualmente degeneri, determinare le eventuali circonferenze tangenti a quelle date».'

Se le tre circonferenze sono tangenti tra di loro, il raggio della quarta è determinato dal teorema di Descartes.


Previous Page Next Page






مسألة أبولونيوس Arabic এপোলোনিয়াসের সমস্যা Bengali/Bangla Problema d'Apol·loni Catalan کێشەی ئاپۆلۆنیوس CKB Apolloniova úloha Czech Apollonisches Problem German Απολλώνιο πρόβλημα Greek Problem of Apollonius English Problema de Apolonio Spanish مسئله آپولونیوس FA

Responsive image

Responsive image