Quadrica

In matematica, e in particolare in geometria, una quadrica (o superficie quadrica) è una (iper-)superficie di uno spazio n-dimensionale sui complessi o sui reali rappresentata da un'equazione polinomiale del secondo ordine nelle variabili spaziali (coordinate). Se le coordinate spaziali sono ${\displaystyle \{x_{1},\ \dots ,\ x_{n}\}}$, allora la generale quadrica nello spazio ${\displaystyle \mathbb {C} ^{n}}$ (o ${\displaystyle \mathbb {R} ^{n}}$) è definita da un'equazione della forma

${\displaystyle \sum _{i,j=1}^{n}B_{ij}x_{i}x_{j}+\sum _{i=1}^{n}E_{i}x_{i}+F=0,}$

dove ${\displaystyle B_{ij}}$ è una matrice (non nulla), ${\displaystyle E}$ un vettore e ${\displaystyle F}$ una costante.

Un punto qualsiasi di una superficie quadrica si definisce iperbolico, parabolico o ellittico a seconda che il piano tangente alla superficie in quel punto tagli la quadrica in due rette reali e distinte, coincidenti o immaginarie coniugate. I punti di una quadrica sono tutti dello stesso tipo, cioè o tutti iperbolici o tutti parabolici o tutti ellittici. Tale caratteristica dipende solo dal segno del determinante della quadrica (invariante nei sistemi di riferimento cartesiani ortogonali) e viene spesso posta in evidenza come aggettivo della quadrica (ad esempio, iperboloide iperbolico).

Attraverso traslazioni e rotazioni ogni quadrica può essere trasformata in una forma "normalizzata", sensibilmente più semplice di quella generale. Ad esempio, l'equazione normalizzata di molte quadriche nello spazio a tre dimensioni (${\displaystyle n=3}$) è:

${\displaystyle \pm {x^{2} \over a^{2}}\pm {y^{2} \over b^{2}}\pm {z^{2} \over c^{2}}\,=\,1}$

Nello spazio euclideo tridimensionale ogni quadrica può essere scritta in una delle seguenti 9 forme normalizzate:

Quadriche non degeneri
Ellissoide	Ellissoide scaleno	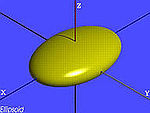${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}$
	Sferoide prolato	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over b^{2}}=1}$
	Sferoide oblato	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1}$
	Sfera	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}=1}$
Paraboloide	Paraboloide ellittico	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z \over c}=0}$
	Paraboloide circolare	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z \over c}=0}$
	Paraboloide iperbolico	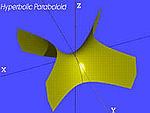${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-{z \over c}=0}$
Iperboloide	Iperboloide ad una falda (iperboloide iperbolico)	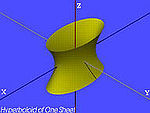${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1}$
	Iperboloide a due falde (iperboloide ellittico)	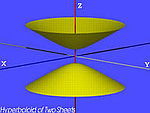${\displaystyle -{x^{2} \over a^{2}}-{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}$
Quadriche degeneri
Cono (a due falde)		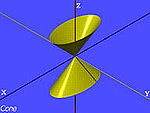${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0}$
Cilindro	Cilindro ellittico	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1}$
	Cilindro circolare	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1}$
	Cilindro parabolico	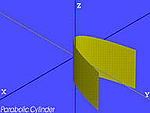${\displaystyle {x^{2} \over 2a}+y=0}$
	Cilindro iperbolico	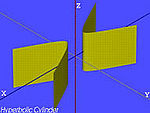${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1}$

Nello spazio proiettivo reale, a meno di una trasformazione proiettiva ci sono tre classi di equivalenza di quadriche:

• il cono, il cilindro e le altre quadriche "degeneri", cioè con curvatura gaussiana zero, sono tra loro equivalenti;
• i due paraboloidi iperbolici e le superfici rigate sono tra loro equivalenti;
• l'ellissoide, il paraboloide ellittico, l'iperboloide a due falde e le rimanenti quadriche sono tra loro equivalenti.

Nello spazio proiettivo complesso tutte le quadriche non degeneri sono tra loro equivalenti, a meno di trasformazioni proiettive.