Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Epiciclo
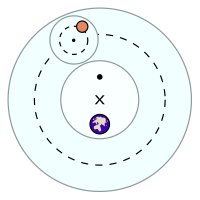
Nos sistemas de astronomia hiparquiana, ptolomaica e copernicana, o epiciclo (do grego antigo ἐπίκυκλος ( epíkuklos) 'sobre o círculo', significando "círculo movendo-se sobre outro círculo")[1] era um modelo geométrico usado para explicar as variações em velocidade e direção do movimento aparente da Lua, do Sol e dos planetas. Em particular, explicou o aparente movimento retrógrado dos cinco planetas conhecidos na época. Secundariamente, também explicou mudanças nas distâncias aparentes dos planetas da Terra.
Foi proposto pela primeira vez por Apolônio de Perga no final do século III a.C. Foi desenvolvido por Apolônio de Perga e Hiparco de Rodes, que o usou extensivamente, durante o século II a.C., depois formalizado e amplamente utilizado por Ptolomeu em seu tratado astronômico do século II d.C., o Almagesto.
O movimento epicíclico é usado no mecanismo de Antikythera, um antigo dispositivo astronômico grego, para compensar a órbita elíptica da Lua, movendo-se mais rápido no perigeu e mais devagar no apogeu do que as órbitas circulares, usando quatro engrenagens, duas delas engatadas de maneira excêntrica que se aproxima bastante da segunda lei de Kepler.
Os epiciclos funcionaram muito bem e foram altamente precisos, porque, como a análise de Fourier mostrou mais tarde, qualquer curva suave pode ser aproximada com precisão arbitrária com um número suficiente de epiciclos. No entanto, eles caíram em desgraça com a descoberta de que os movimentos planetários eram em grande parte elípticos a partir de um referencial heliocêntrico, o que levou à descoberta de que a gravidade obedecendo a uma simples lei do quadrado inverso poderia explicar melhor todos os movimentos planetários.
- ↑ «epicycle | Etymology, origin and meaning of epicycle by etymonline». www.etymonline.com (em inglês). Consultado em 20 de maio de 2023
Previous Page Next Page


