Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.
Law of large numbers
The law of large numbers, or LLN for short,[1] is a theorem from statistics. It states that if a random process is repeatedly observed, then the average of the observed values will be stable in the long run. This means that as the number of observations increases, the average of the observed values will get closer and closer to the expected value.
For example, when rolling dice, the numbers 1, 2, 3, 4, 5 and 6 are possible outcomes. They are all equally likely. The population mean (or "expected value") of the outcomes is:
- (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5.
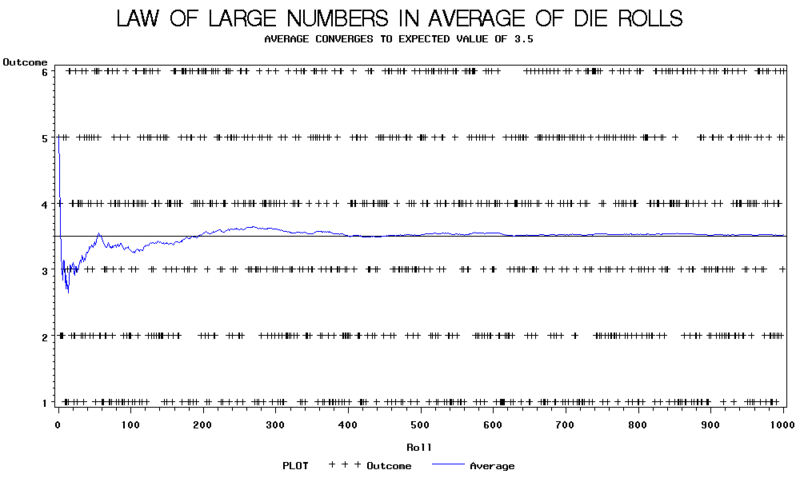
The following graph shows the results of an experiment of rolls of a die. In this experiment, it can be seen that the average of die rolls varies wildly at first, but as predicted by the LLN, the average stabilizes around the expected value of 3.5 as the number of observations become large.
- ↑ "List of Probability and Statistics Symbols". Math Vault. 2020-04-26. Retrieved 2020-10-14.
Previous Page Next Page