Our website is made possible by displaying online advertisements to our visitors.
Please consider supporting us by disabling your ad blocker.

Responsive image

Chaos theory

For other uses, see Chaos theory (disambiguation).
A plot of the Lorenz attractor for values r = 28, σ = 10, b = ⁠8/3⁠
An animation of a double-rod pendulum at an intermediate energy showing chaotic behavior. Starting the pendulum from a slightly different initial condition would result in a vastly different trajectory. The double-rod pendulum is one of the simplest dynamical systems with chaotic solutions.

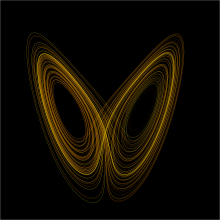
Chaos theory (or chaology[1]) is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities.[2] Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization.[3] The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions).[4] A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.[5][6]: 181–184 [7]

Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general.[8] This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution[9] and is fully determined by their initial conditions, with no random elements involved.[10] In other words, the deterministic nature of these systems does not make them predictable.[11][12] This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:[13]

Chaos: When the present determines the future but the approximate present does not approximately determine the future.

Chaotic behavior exists in many natural systems, including fluid flow, heartbeat irregularities, weather and climate.[14][15][9] It also occurs spontaneously in some systems with artificial components, such as road traffic.[3] This behavior can be studied through the analysis of a chaotic mathematical model or through analytical techniques such as recurrence plots and Poincaré maps. Chaos theory has applications in a variety of disciplines, including meteorology,[9] anthropology,[16] sociology, environmental science, computer science, engineering, economics, ecology, and pandemic crisis management.[17][18] The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory and self-assembly processes.

  1. ^ chaology. (2024, June 22). Wiktionary. Retrieved 07:12, November 17, 2024 from https://en.wiktionary.org/w/index.php?title=chaology&oldid=80484855
  2. ^ "chaos theory | Definition & Facts". Encyclopedia Britannica. Retrieved 2019-11-24.
  3. ^ a b "What is Chaos Theory? – Fractal Foundation". Retrieved 2019-11-24.
  4. ^ Weisstein, Eric W. "Chaos". mathworld.wolfram.com. Retrieved 2019-11-24.
  5. ^ Boeing, Geoff (26 March 2015). "Chaos Theory and the Logistic Map". Retrieved 2020-05-17.
  6. ^ Lorenz, Edward (1993). The Essence of Chaos. University of Washington Press. ISBN 978-0-295-97514-6.
  7. ^ Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Cui, Jialin; Faghih-Naini, Sara; Paxson, Wei; Atlas, Robert (2022-07-04). "Three Kinds of Butterfly Effects within Lorenz Models". Encyclopedia. 2 (3): 1250–1259. doi:10.3390/encyclopedia2030084. ISSN 2673-8392. Text was copied from this source, which is available under a Creative Commons Attribution 4.0 International License.
  8. ^ Kellert, Stephen H. (1993). In the Wake of Chaos: Unpredictable Order in Dynamical Systems. University of Chicago Press. p. 32. ISBN 978-0-226-42976-2.
  9. ^ a b c Bishop, Robert (2017), "Chaos", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2017 ed.), Metaphysics Research Lab, Stanford University, retrieved 2019-11-24
  10. ^ Kellert 1993, p. 56
  11. ^ Kellert 1993, p. 62
  12. ^ Werndl, Charlotte (2009). "What are the New Implications of Chaos for Unpredictability?". The British Journal for the Philosophy of Science. 60 (1): 195–220. arXiv:1310.1576. doi:10.1093/bjps/axn053. S2CID 354849.
  13. ^ Danforth, Christopher M. (April 2013). "Chaos in an Atmosphere Hanging on a Wall". Mathematics of Planet Earth 2013. Retrieved 12 June 2018.
  14. ^ Cite error: The named reference Lorenz1961 was invoked but never defined (see the help page).
  15. ^ Ivancevic, Vladimir G.; Tijana T. Ivancevic (2008). Complex nonlinearity: chaos, phase transitions, topology change, and path integrals. Springer. ISBN 978-3-540-79356-4.
  16. ^ Mosko M.S., Damon F.H. (Eds.) (2005). On the order of chaos. Social anthropology and the science of chaos. Oxford: Berghahn Books.
  17. ^ Piotrowski, Chris. "Covid-19 Pandemic and Chaos Theory: Applications based on a Bibliometric Analysis". researchgate.net. Retrieved 2020-05-13.
  18. ^ Weinberger, David (2019). Everyday Chaos – Technology, Complexity and How We're Thriving in a New World of Possibility. Harvard Business Review Press. ISBN 9781633693968.

Previous Page Next Page






Chaosteorie AF نظرية فوضى الكون Arabic نضرية الروينة ARY Teoría del caos AST Xaos nəzəriyyəsi AZ Хаос теорияһы BA Теория на хаоса Bulgarian বিশৃঙ্খলা তত্ত্ব Bengali/Bangla Teoria del caos Catalan تیۆریی شێواوی CKB

Responsive image

Responsive image