
Back تجزئة (نظرية الأعداد) Arabic Хисеп пайлавĕ CV Partición (teoría de números) Spanish افراز عدد صحیح FA Partition d'un entier French חלוקה (קומבינטוריקה) HE Partíció (számelmélet) Hungarian Partisi (teori bilangan) ID Partizione di un intero Italian 自然数の分割 Japanese

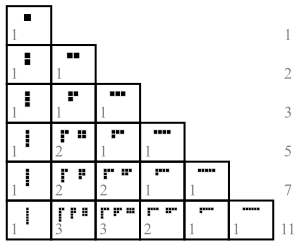
In number theory and combinatorics, a partition of a non-negative integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. (If order matters, the sum becomes a composition.) For example, 4 can be partitioned in five distinct ways:
- 4
- 3 + 1
- 2 + 2
- 2 + 1 + 1
- 1 + 1 + 1 + 1
The only partition of zero is the empty sum, having no parts.
The order-dependent composition 1 + 3 is the same partition as 3 + 1, and the two distinct compositions 1 + 2 + 1 and 1 + 1 + 2 represent the same partition as 2 + 1 + 1.
An individual summand in a partition is called a part. The number of partitions of n is given by the partition function p(n). So p(4) = 5. The notation λ ⊢ n means that λ is a partition of n.
Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representation theory in general.