
 =
= 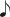 ), in a piece by J.S. Bach. Slow introduction followed by an allegro traditionally taken at double the speed. Sixteenth notes in the old tempo prepare for eighth notes in the new tempo.[1]
), in a piece by J.S. Bach. Slow introduction followed by an allegro traditionally taken at double the speed. Sixteenth notes in the old tempo prepare for eighth notes in the new tempo.[1] In music, metric modulation is a change in pulse rate (tempo) and/or pulse grouping (subdivision) which is derived from a note value or grouping heard before the change. Examples of metric modulation may include changes in time signature across an unchanging tempo, but the concept applies more specifically to shifts from one time signature/tempo (metre) to another, wherein a note value from the first is made equivalent to a note value in the second, like a pivot or bridge. The term "modulation" invokes the analogous and more familiar term in analyses of tonal harmony, wherein a pitch or pitch interval serves as a bridge between two keys. In both terms, the pivoting value functions differently before and after the change, but sounds the same, and acts as an audible common element between them. Metric modulation was first described by Richard Franko Goldman[2] while reviewing the Cello Sonata of Elliott Carter, who prefers to call it tempo modulation.[3] Another synonymous term is proportional tempi.[4]
A technique in which a rhythmic pattern is superposed on another, heterometrically, and then supersedes it and becomes the basic metre. Usually, such time signatures are mutually prime, e.g., 4
4 and 3
8, and so have no common divisors. Thus the change of the basic metre decisively alters the numerical content of the beat, but the minimal denominator (1
8 when 4
4 changes to 3
8; 1
16 when, e.g., 5
8 changes to 7
16, etc.) remains constant in duration.[5]
- ^ Weisberg 1996, 51–52.
- ^ Goldman 1951.
- ^ Schiff 1998, 23.
- ^ Mead 2007, 65.
- ^ Slonimsky 2000.
