Mutual information

Information theory
Entropy Differential entropy Conditional entropy Joint entropy Mutual information Directed information Conditional mutual information Relative entropy Entropy rate Limiting density of discrete points
Asymptotic equipartition property Rate–distortion theory
Shannon's source coding theorem Channel capacity Noisy-channel coding theorem Shannon–Hartley theorem
v t e

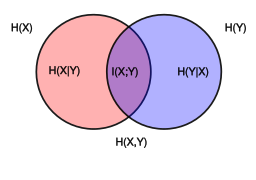
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the "amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable.

Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair ${\displaystyle (X,Y)}$ is from the product of the marginal distributions of ${\displaystyle X}$ and ${\displaystyle Y}$. MI is the expected value of the pointwise mutual information (PMI).

The quantity was defined and analyzed by Claude Shannon in his landmark paper "A Mathematical Theory of Communication", although he did not call it "mutual information". This term was coined later by Robert Fano.^[2] Mutual Information is also known as information gain.