
Back Κανονικό πολύτοπο Greek Regula hiperpluredro EO Politopo regular Spanish Polytope régulier French Politopo regolare Italian 正多胞体 Japanese 정다포체 Korean Regelmatige polytoop Dutch Regulær polytop NB Politop regulat Romanian
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (July 2014) |
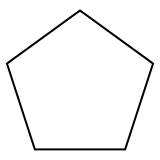 A regular pentagon is a polygon, a two-dimensional polytope with 5 edges, represented by Schläfli symbol {5}. |
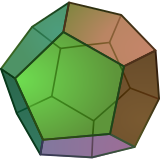 A regular dodecahedron is a polyhedron, a three-dimensional polytope, with 12 pentagonal faces, represented by Schläfli symbol {5,3}. |
 A regular 120-cell is a polychoron, a four-dimensional polytope, with 120 dodecahedral cells, represented by Schläfli symbol {5,3,3}. (shown here as a Schlegel diagram) |
 A regular cubic honeycomb is a tessellation, an infinite polytope, represented by Schläfli symbol {4,3,4}. |
 The 256 vertices and 1024 edges of an 8-cube can be shown in this orthogonal projection (Petrie polygon) | |
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.
Regular polytopes are the generalised analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both mathematicians and non-mathematicians.
Classically, a regular polytope in n dimensions may be defined as having regular facets ([n–1]-faces) and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.
A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ..., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.